Статистическая оценка биогенного риска для человеческой популяции со стороны новых вирусных инфекций на примере COVID-19

Введение. Понимание эпидемической кривой и пространственно-временной динамики распространения вируса SARS-CoV-2 необходимо, во-первых, для оценки его эпидемиологических характеристик. Кроме того, оно позволяет прорабатывать и реализовать меры противодействия распространению коронавирусной инфекции (COVID-19), рационально распределять ресурсы. Цель данной работы — создание математической модели эпидемического процесса, которая дает возможность объяснить наблюдаемую динамику, прогнозировать распространение инфекции и оценивать достоверность таких прогнозов. COVID-19 — это новое заболевание, поэтому его изучают посредством детального мониторинга заражений и смертности. Результаты интерпретируют с помощью математических моделей и связанных с ними аналитических подходов [1–2]. Знание эволюционных закономерностей и числовых показателей эпидемических болезней позволяет своевременно купировать процесс, задействуя официальные медицинские и другие организационные ресурсы [3–4]. Достоверный фактический материал по заболеваемости COVID-19 и связанной с ним смертности в мировом масштабе [5] публикуется на ресурсе worldometers.info[1] (рассматривается период с 12.02.2020 по 22.09.2021). Использование этих данных в некоторой степени снижает погрешности регионального и временного мониторинга, но может препятствовать выявлению локальных динамических параметров процесса. Однако продолжительность зафиксированных в [5] наблюдений позволяет надеяться, что указанный недостаток нивелирует техника анализа временных рядов [6].

Имеющиеся в нашем распоряжении данные о динамике заболеваемости и смертности ковид-положительных пациентов с 12.02.2020 по 22.09.2021 взяты из worldometers.info. На их основе авторы построили диаграммы (рис. 1–2).

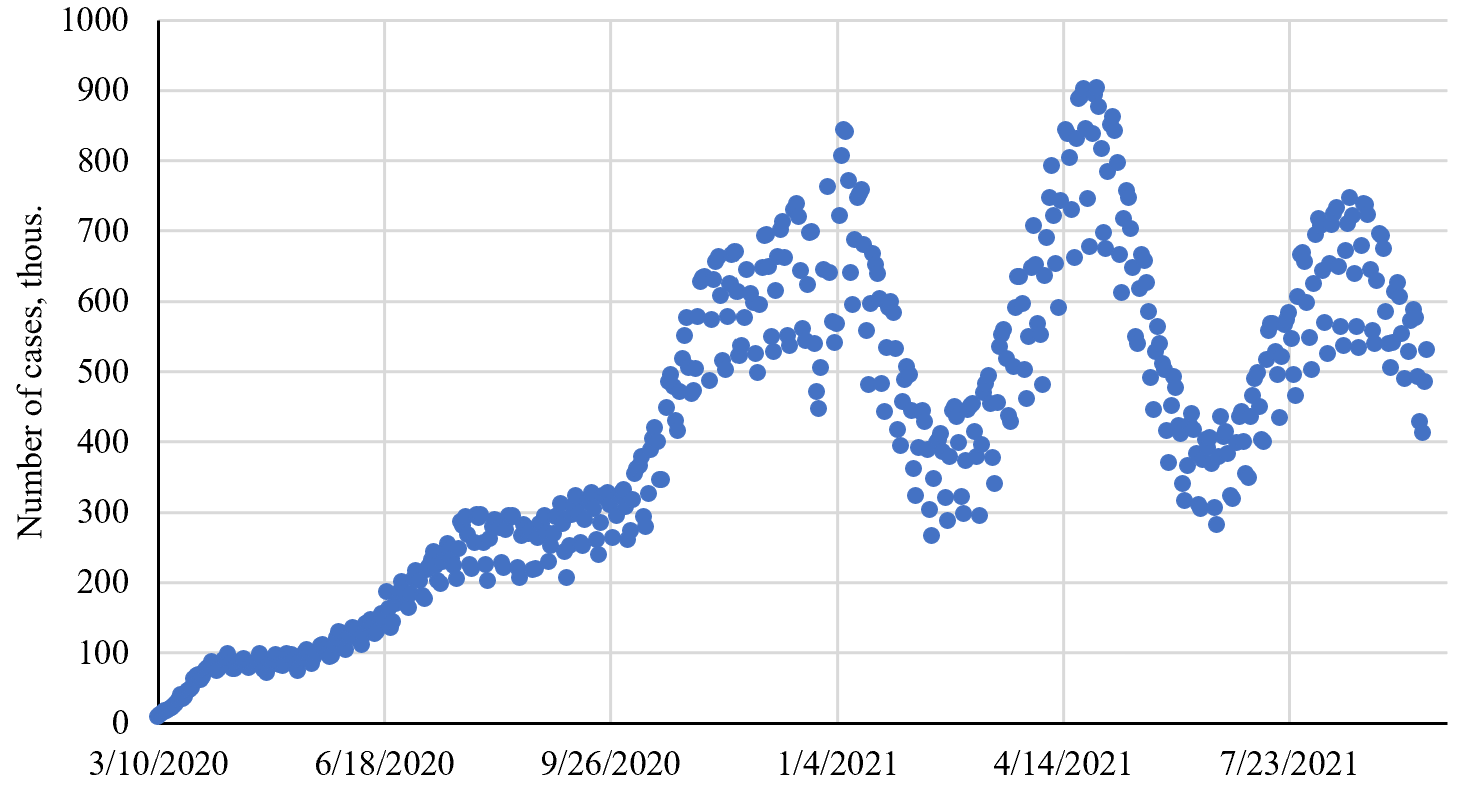
Рис. 1. Данные по заболеваемости COVID-19 (рисунок авторов)

Авторы поставили задачу проанализировать связь смертности (зафиксированной впоследствии) с этапом пандемии и уровнем заболеваемости. Для этого исходные данные группировались по кварталам (3 месяца). На рис. 2 они обозначены точками определенного цвета. Такой подход визуализирует представление преобразованных данных о смертности, в которых моменты смерти явно не фигурируют.

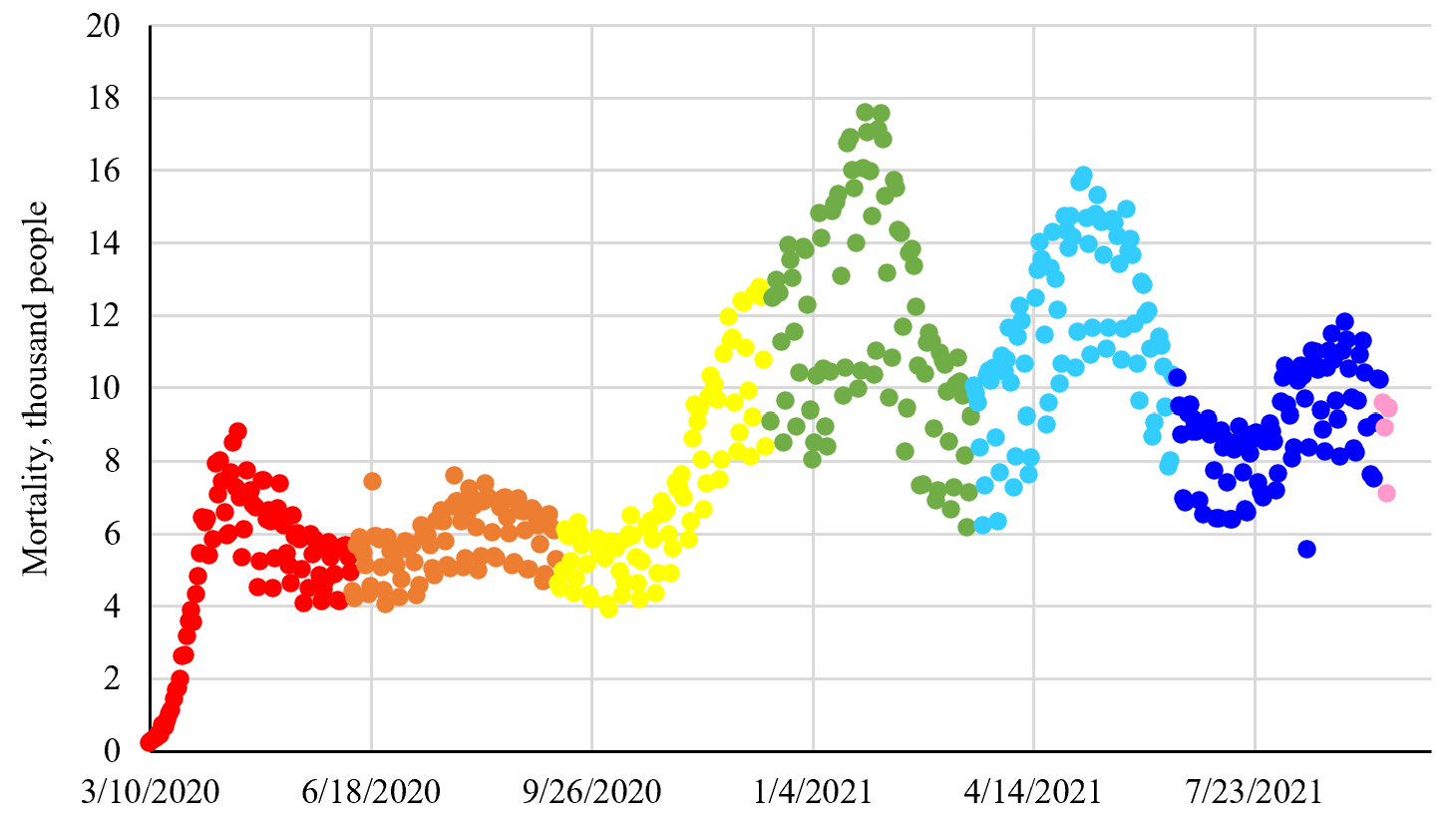
Рис. 2. Фактические данные по смертности ковид-положительных пациентов. Красными точками обозначен период пандемии с 12.02.20 по 9.06.20; оранжевыми — с 10.06.20 по 10.09.20; желтыми — с 11.09.20 по 14.12.20; зелеными — с 16.12.20 по 17.03.21; голубыми — с 18.03.21 по 17.06.21; синими — с 18.06.21 по 18.09.21; сиреневыми — с 19.09.21 по 22.09.21 (рисунок авторов)

Материалы и методы. Рассмотренные данные представляют собой композицию регулярной и случайной составляющих. В регулярной выделяются апериодическая и периодическая компоненты. Соответственно, анализ, интерпретация и прогнозирование в данном случае выполняются классическими средствами исследования временных рядов [6]. Речь идет о последовательном выделении тренда (апериодической составляющей), циклической и шумовой (случайной) компонент. Каждая из них с математической точки зрения характеризуется амплитудными и (или) временными параметрами [7]. Последовательно выделим эти компоненты из фактических данных, затем опишем результаты.

В качестве математического инструментария для анализа и прогнозирования динамики COVID-19 выбрали классическую технику исследования временных рядов Ф(t) [6]. Она реализуется в несколько этапов, которые нацелены на последовательное выявление регулярной P(t), колебательной П(t) и случайной  составляющих тренда. При этом, как правило, принимается во внимание гипотеза, что равно нулю среднее по времени значение двух последних составляющих временного ряда

                                                                         Ф(t) = P(t) + П(t) + , (1)

то есть выполняется соотношение:

 (2)

Регулярная составляющая P(t) выделяется первой. Алгоритмической основой здесь служит теория аппроксимации функции [7]. Она базируется на идее отыскания кривой заданного вида, максимально близкой к облаку точек, отображающих временной ряд. При этом требуется удачно выбрать шаблон аппроксимирующей ряд функции. С одной стороны, это исключительно творческая задача. С другой, она требует глубоких знаний в области математического анализа. Затем регулярная составляющая исключается из (1) и анализируется комбинация .

Важные характеристики такого остаточного слагаемого: период и форма [8]. Для выявления периода оставляющей П(t) используется техника корреляционного и Фурье-анализа. В рамках автокорреляционного анализа период функции П(t) — это величина , удовлетворяющая условию

(3)

где [0…T] — интервал наблюдения за величиной П(t).

Использование для той же цели дискретного преобразования Фурье позволяет локализовать величину   в узком интервале. Зная , можно выявить форму периодической составляющей, но часто исследователи ограничиваются первой гармоникой.

Заключительный этап — выявление статистических свойств . Для этого наиболее удобен метод моментов [9]. Он работает так: сравниваются фактические моменты шума ряда с моментами модельных шумов, задаваемых известными функциями распределения . Описанная схема анализа временного ряда Ф(t) показана на рис. 3.

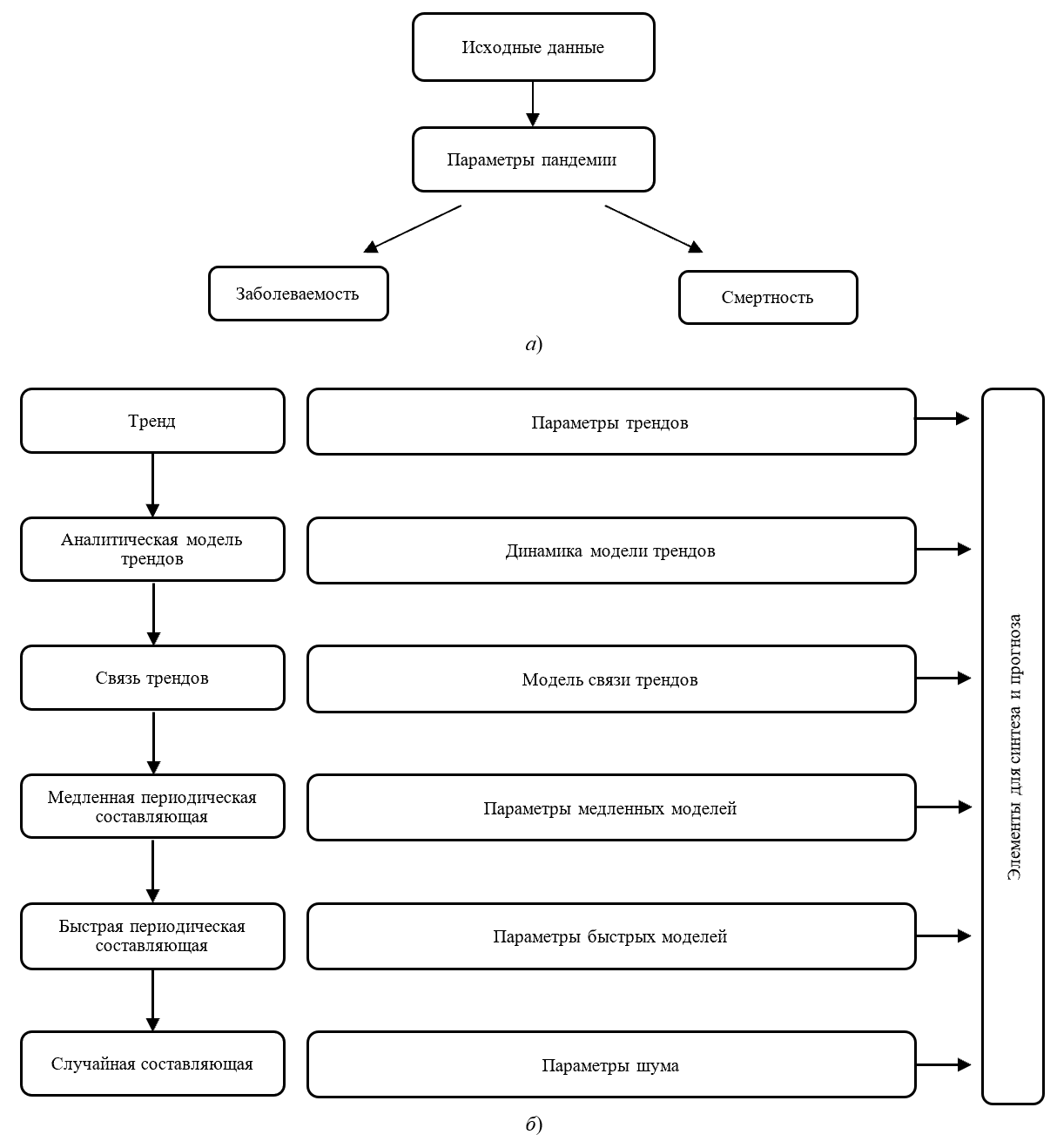
Рис. 3. Анализ временного ряда заболеваемости и смертности ковид-положительных пациентов: а — этапы по фокусу изысканий; б — алгоритм исследования (рисунок авторов)

Результаты исследования. Известно, что любой эпидемический процесс в начальной стадии характеризуется экспоненциальной во времени динамикой [10], т. е.

, (4)

где  — число заболевших;  и  — некоторые положительные числа.

Дальнейшее развитие эпидемии может происходить по оптимистичному или пессимистичному сценарию. В первом случае эпидемия достигает некоторого пика и сходит на нет. Зависимость численности заболевших в некоторый момент имеет вид:

, (5)

где A, B, C — коэффициенты модели; ch — гиперболический косинус.

Этому сценарию соответствует дифференциальное уравнение:

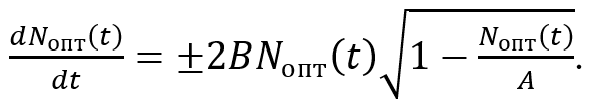 (6)

Здесь знак «плюс» реализуется при  вплоть до момента t*, при котором . Начиная с этого момента в формуле (6) реализуется знак «минус». Согласно (6), по достижении некоторого критического числа заболевших  заболеваемость начнет монотонно снижаться.

Пессимистичный сценарий подразумевает, что развивающаяся изначально по экспоненте эпидемия со временем также экспоненциально выходит на плато, т. е. возбудитель остается в пораженной им популяции. Это можно описать эволюционной зависимостью

, (7)

которой соответствует дифференциальное уравнение:

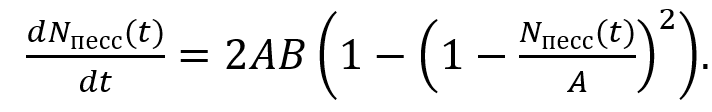(8)

Здесь th  — гиперболический тангенс. В (7) и (8) множитель 2 добавлен из соображений совпадения стартовой асимптотики, т. е. для выполнения естественного соотношения:

(9)

Промежуточный сценарий эпидемии сочетает элементы двух рассмотренных и предполагает следующие стадии:

1) первичный экспоненциальный рост;

2) насыщение и последующий спад;

3) выход на ненулевое плато.

Динамику заболеваемости в этом случае описывает линейное сопряжение формул (5) и (7) с весом D:

, (10)

где D — коэффициент, отражающий вклад оптимистичного и пессимистичного сценария в совокупный процесс.

Решению (10) соответствует нелинейное дифференциальное уравнение высокого порядка [11], которое опустим из-за его громоздкости.

Для нахождения коэффициентов А, В, С, D необходимо решить задачу математического программирования [12] в ее общем виде:

(11)

где  и t_i — соответственно заболеваемость и момент ее фиксации.

Условие экстремума (11) отвечает обобщенному сценарию эпидемии. В частных случаях моделей (5) и (7) к (11) следует добавить ограничения D = 1 или

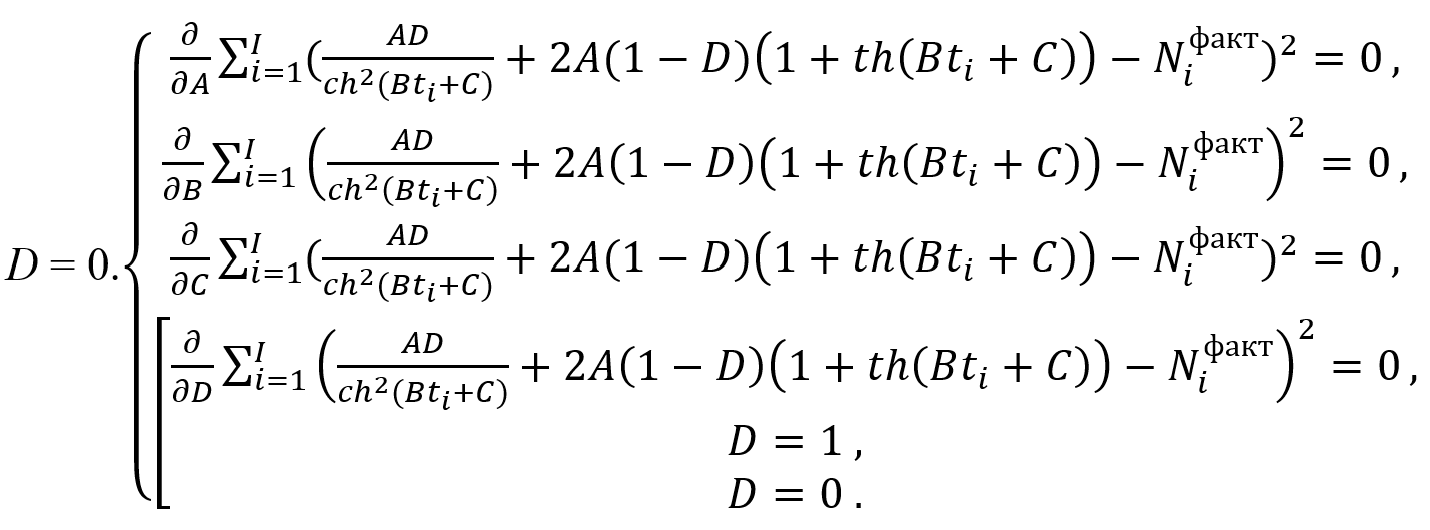(12)

Здесь  обозначен частный дифференциал. Можно также строго доказать, что система (12) эквивалентна переопределенной системе алгебраических уравнений:

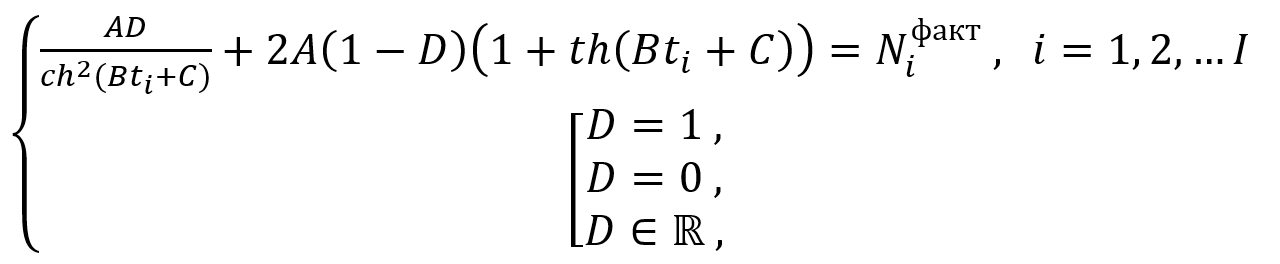(13)

варианты которой соответствуют описанным сценариям.

Результаты выявления трендовой зависимости P(t) с использованием встроенных функций MS Excel [13] для всех сценариев эпидемической динамики приведены на рис. 2 и в таблице 1.

Таблица 1

Числовые характеристики трендовой модели заболеваемости COVID-19

Как видно из данных таблицы, обобщенная модель (10) лучше описывает реальную ситуацию. Однако у нее есть существенный недостаток. Это сравнительная сложность и невозможность явно выписать нелинейные дифференциальные уравнения, отвечающие динамике COVID-19. В данном отношении пессимистичная модель привлекает своей простотой и, соответственно, возможностями усовершенствования.

Для идентификации колебательной составляющей в данных о смертности при COVID-19 (рис. 3) выберем следующую модель. Предположим, что реальные данные колеблются около линии тренда. В нашем случае это модели (5)–(6), (7)–(8) и (10) с амплитудой α, круговой частотой β и начальной фазой γ. Такая регулярная модель динамики эпидемии декомпозируется и описывается уравнением:

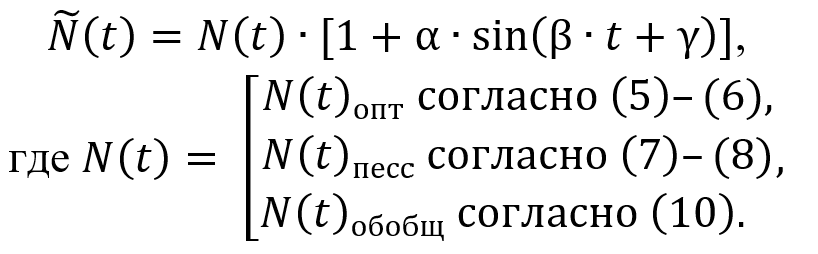(14)

Для отыскания параметров колебательной модели (14) необходимо решить следующую оптимизационную задачу [12]:

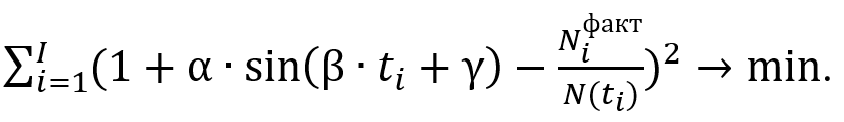  (15)

Если рассматривать (15) как функцию переменных α, β, γ, необходимое условие экстремума принимает вид [8]:

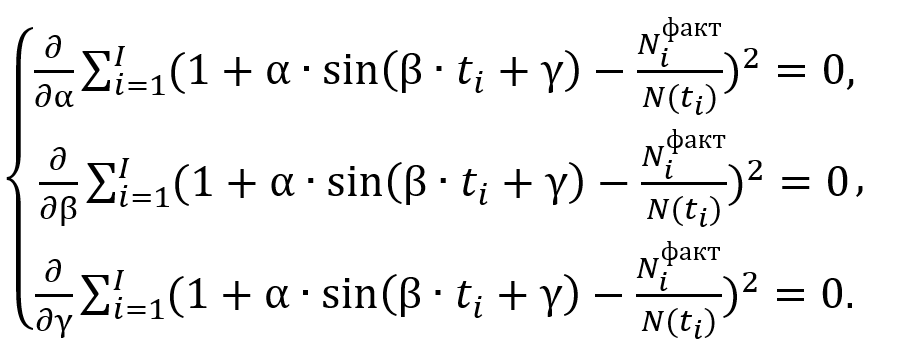 (16)

Решение задачи (16) совпадает с решением переопределенной системы уравнений:

(17)

Однако практическая реализация алгоритмов (16) и (17) затруднена их неустойчивостью, обусловленной особенностями задачи [7]. В данном случае более устойчивым оказывается алгоритм, основанный на отыскании параметров модели, обеспечивающих наилучшую корреляцию фактических данных [9] и модельной функции  :

(18)

Решение (18), полученное средствами Excel [9] для вариантов модели  (5)–(6), (7)–(8) и (10), приведено в таблице 2.

Таблица 2

Числовые характеристики модели колебаний заболеваемости COVID-19

Представленные в таблице 2 числовые показатели адекватности моделей ξ и σ свидетельствуют, что обобщенная модель лучше соответствует фактическим данным. В то же время она значительно сложнее пессимистичной при несущественном улучшении точности. Таким образом, следует признать преимущество пессимистичной модели. Она обладает оптимальной сложностью математического описания эпидемии COVID-19, допускающей простую интерпретацию и легкость усовершенствования.

Важно отметить, что для любого тренда характерна периодичность в 127 ± 0,5 дней. Этот результат хорошо согласуется с данными автокорреляционного и спектрального анализа колебательной составляющей функции   (рис. 4). Таким образом зафиксировано, что всплески заболевания происходят через 124 и 110 дней. Значит, заболевание носит сезонный характер с периодом 1/3 года.

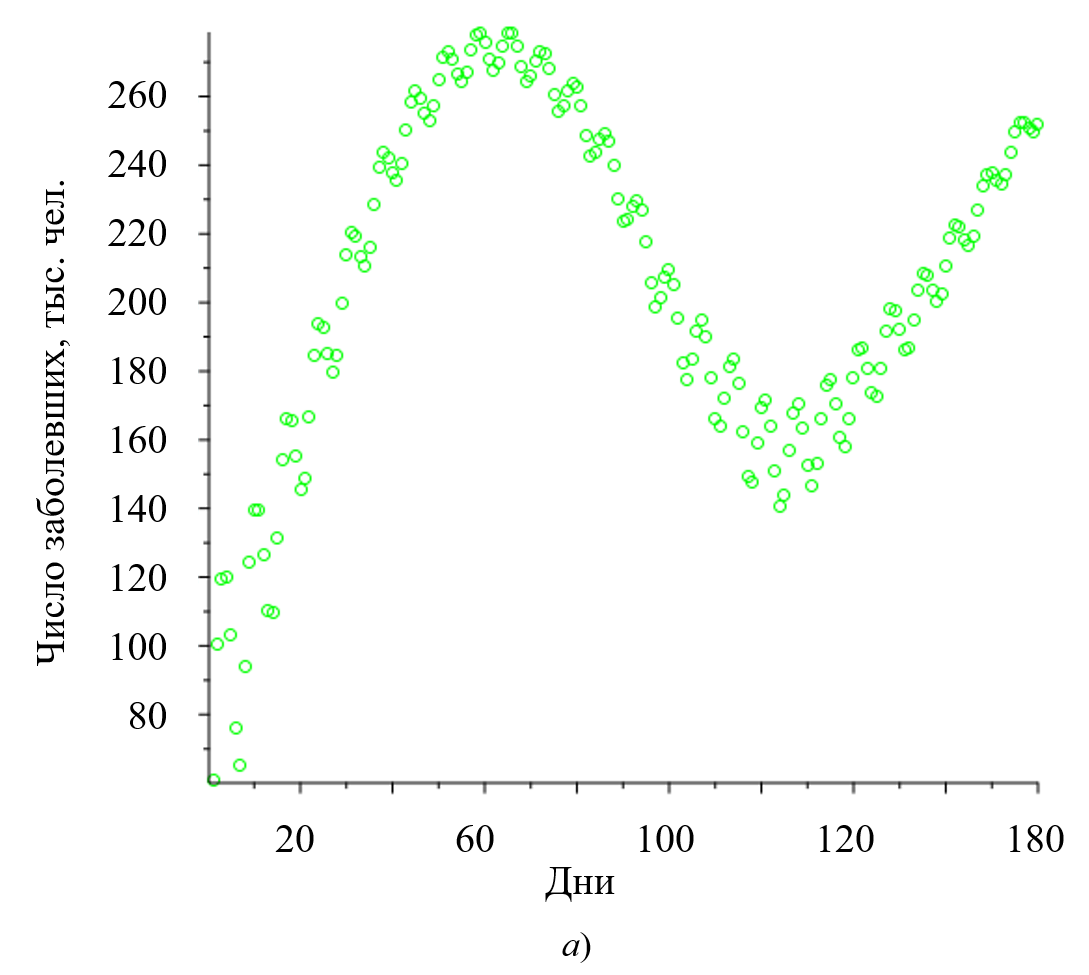
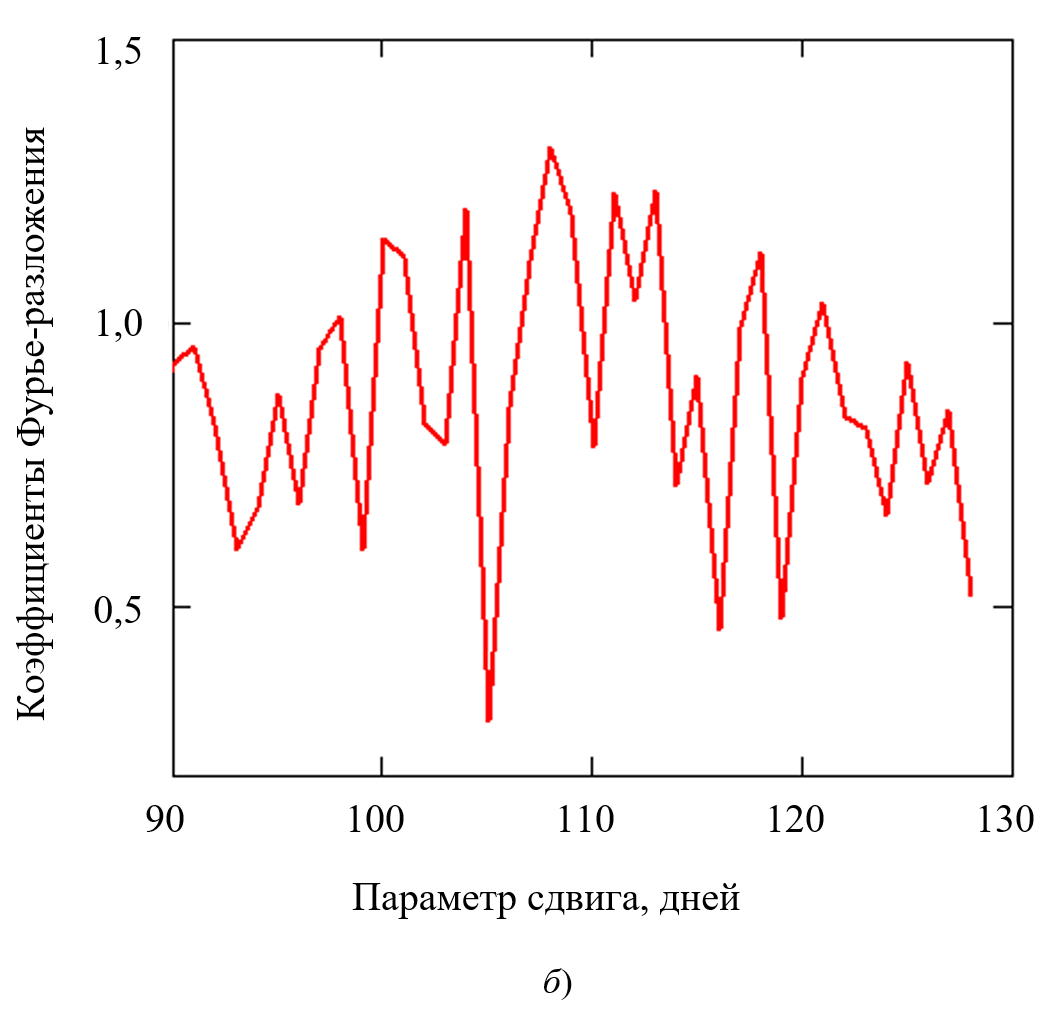
Рис. 4. Данные автокорреляционного и спектрального анализа колебательной составляющей: а — отличие динамики заболеваемости при сдвиге на различное число дней; б — коэффициенты спектрального разложения заболеваемости (рисунок авторов)

Сопоставление данных таблиц 1 и 2 позволяет оценить относительную роль колебательной и шумовой составляющей. Если считать их независимыми (ортогональными) и воспользоваться известным соотношением можно убедиться, что вклады периодической и случайной составляющих сопоставимы.

Вычитая модельные значения заболеваемости из наблюдаемых (или наоборот), выделяем оставшуюся шумовую компоненту модели. Результат для пессимистичного сценария показан на рис. 5.

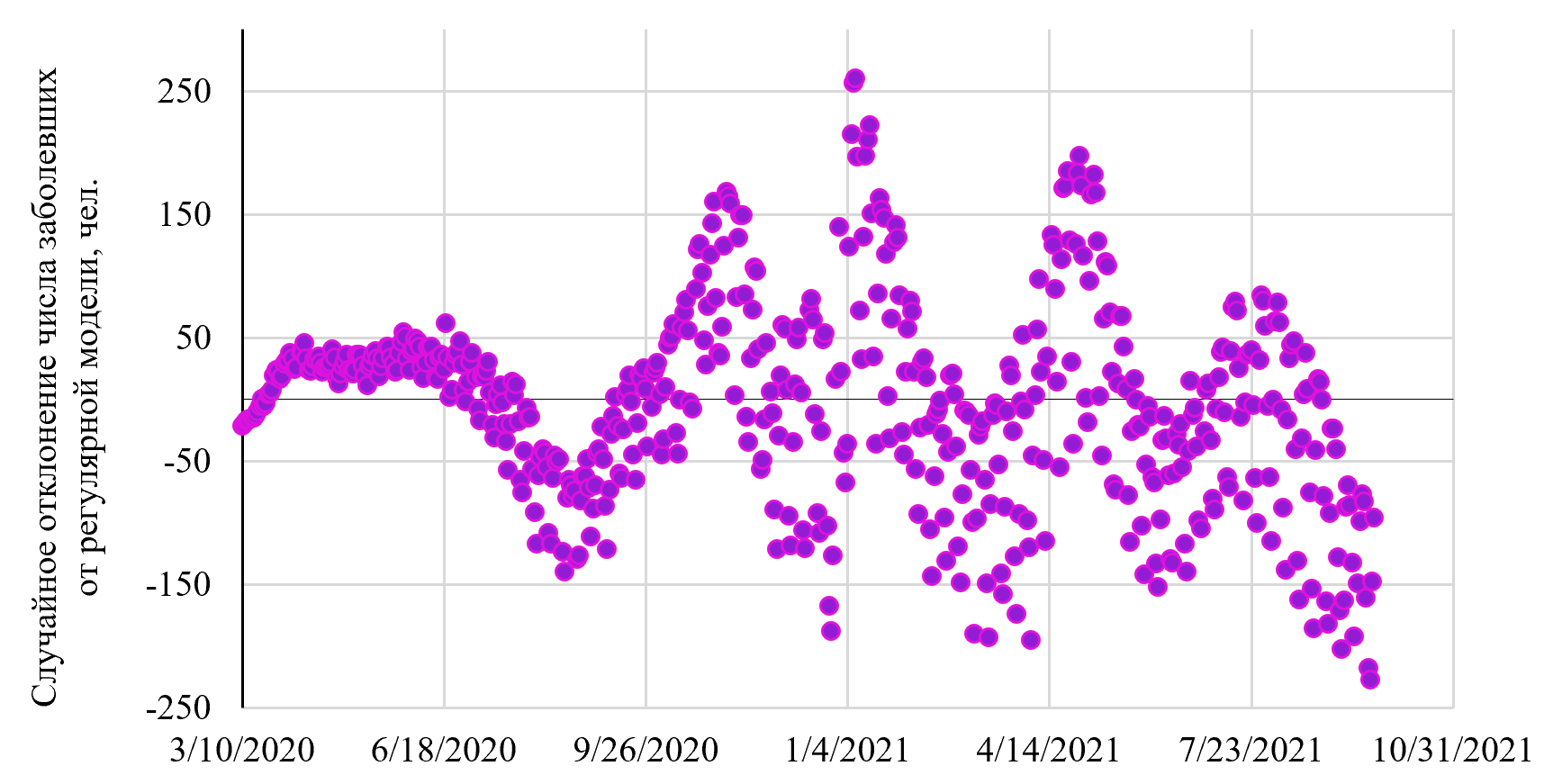
Рис. 5. Шумовая составляющая в пессимистичной модели (рисунок авторов)

Числовые характеристики приведенных на рисунке данных соответствуют нормальному Гауссову распределению [9] с математическим ожиданием «ноль» и среднеквадратичным отклонением 80 тыс. заболевших в сутки, что подтверждается данными числовой идентификации:

– математическое ожидание M = –2,87;

– среднеквадратичное отклонение σ = 79,9;

– асимметрия Skewness = 0,0085;

– эксцесс Kurtosis = 3,51.

Таким образом, выполненная в данной работе идентификация математической модели , предположительно, позволяет прогнозировать заболеваемость на весь срок развития эпидемии [5].

Аналогично анализировалась динамика смертности ковид-положительных пациентов с 12.02.2020 по 22.09.2021 (рис. 3). Учитывая, что летальный исход является вероятным результатом заражения, логично представить модель смертности:

(19)

Или с учетом аппроксимации заболеваемости:

 (20)

Здесь M обозначена смертность; — вероятность умереть от данного заболевания; — наиболее вероятное время от заражения человека до его смерти. Фигурирующие в модели смертности (19) числовые параметрыи будем находить, минимизируя функционал отклонения:

 (21)

с учетом естественных ограничений  .

Особенность решения задачи (21) состоит в том, что одна из искомых переменных фигурирует в верхнем индексе суммирования. Поэтому решение оптимизационной задачи получим в два этапа. Первый основывается на необходимом условии экстремума :

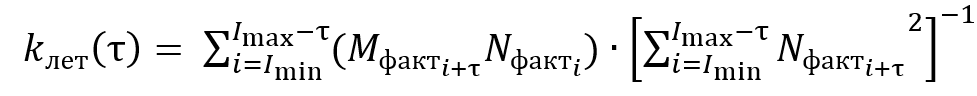(22)

для всего диапазона . Затем выберем пару значений , обеспечивающую минимальное значение (21).

Важно отметить, что  принимаем равным 150 дням. Допущение обусловлено тем, что первые месяцы статистика заболеваемости и смертности [5] представляется недостаточно полной и достоверной.

Решив задачу (21), получим: и день. Более подробно связь смертности с заболеваемостью демонстрирует коррелограмма данных  (рис. 6).

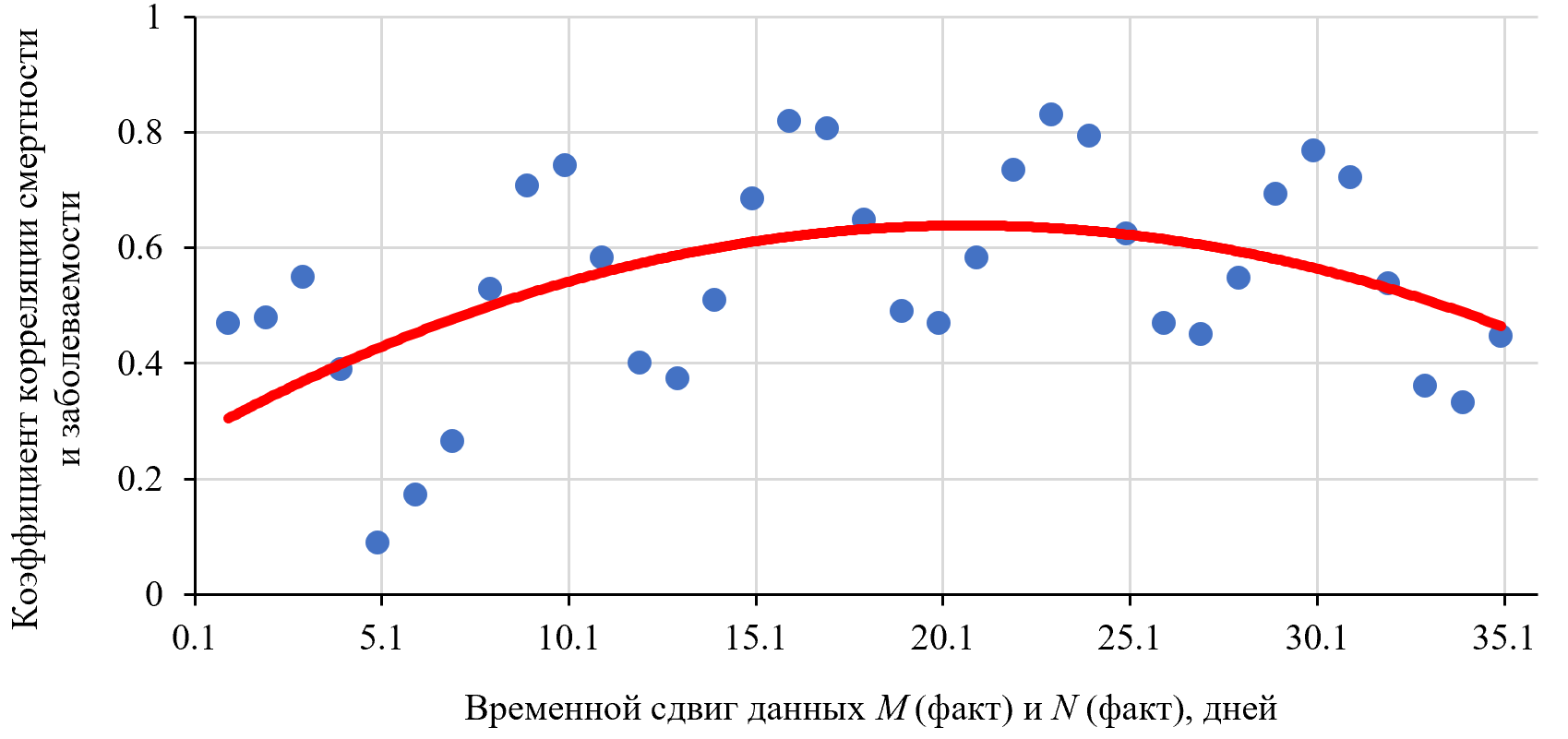
Рис. 6. Коррелограмма смертности и заболеваемости в зависимости от параметра сдвига τ (рисунок авторов)

Анализ тренда показывает вероятность летального исхода при COVID-19 на 21-й день после заражения. Кроме того, очевидна периодичность риска смерти. Очищенные от тренда вариации риска смерти визуализированы на рис. 7.

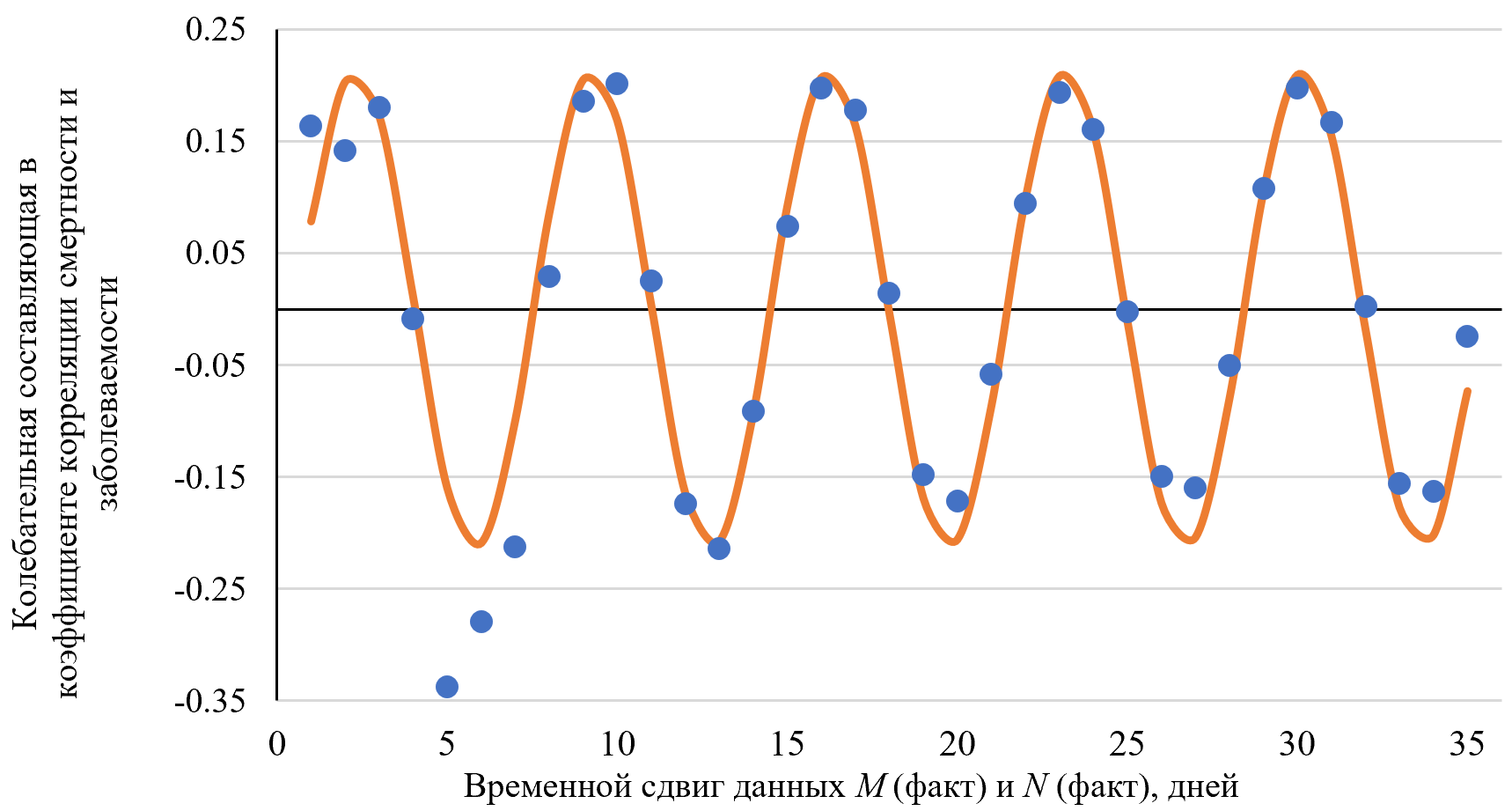
Рис. 7. Быстрая колебательная составляющая в коррелограмме смертности и заболеваемости (рисунок авторов)

Согласно данным рис. 7, риск смерти при COVID-19 колеблется вокруг указанного выше среднего значения с периодом 7 дней, что полностью соответствует цикличности работы медицинских учреждений по всему миру. Аппроксимирующая данные рис. 7 аналитическая зависимость имеет вид:

 (23)

где быстрая составляющая смертности.

Обсуждение и заключения. Ниже перечислены основные итоги работы.

1. Сконструированы и инициализированы модели заболеваемости и смертности при COVID-19.
2. Установлено, что распространение коронавирусной инфекции повторяется три раза в год.
3. Смертность в среднем постоянна и содержит два колебательных элемента. Периодичность первого соответствует периодичности заболеваемости, а периодичность второго — регламенту работы медицинских учреждений.
4. По интервалу наблюдений с 12.02.2020 по 22.09.2021 можно сделать вывод, что сценарий развития эпидемии близок к пессимистическому.
5. Случайная составляющая в моделях заболеваемости и смертности оказалась на уровне сезонных колебаний.

Появившиеся в декабре 2021 года статистические данные показали, что известные штаммы COVID-19 практически вытеснены новым — омикроном. Его заразность в 3 5 раза выше, смертность во столько же раз ниже. Данное обстоятельство диктует необходимость совершенствования предлагаемых динамических моделей эпидемии с учетом вирус-конкурентного эффекта. Это цель следующих исследований коллектива авторов.

Полученные результаты принципиально позволяют не только прогнозировать дальнейшую динамику пандемии, но и формулировать практически значимые рекомендации. Например, в качестве оптимальных сроков антиковидной вакцинации «Спутником V» предлагаются следующие интервалы (ежегодно): 05.02–15.02, 17.05–28.05, 24.09–5.10.

¹Сovid-19 coronavirus pandemic / [International team of developers, researchers, and volunteers] // https://www.worldometers.info  : [website]. URL: https://www.worldometers.info/coronavirus/ (Accessed: 01/10/2023).