Scroll to:
Refinement of the Ground Forest Fire Model Taking into Account Convective Turbulence
https://doi.org/10.23947/2541-9129-2025-9-1-14-21
EDN: XCYIOF
Abstract
Introduction. The scientific literature is actively discussing the topic of mathematical modeling of forest fires development to predict the speed of spread and area covered. From the perspective of turbulent processes, the height and deflection of fire, smoke, and hot air columns, as well as the spread of combustion particles and rational directions for extinguishing the fire, are evaluated. However, existing models do not provide a clear understanding of how turbulence occurs during the transition of a fire from a near-surface to an unsteady surface layer and higher. In other words, calculating the transition from ground fire to its more intense form remains a challenge. Addressing this gap is an urgent scientific and practical task. The aim of this study is to refine the equations of mathematical models for predicting the spread of forest fires, in order to better control these incidents, which will ultimately help reduce risks and damage from them.
Materials and Methods. To achieve this goal, we studied works covering different approaches, both theoretical and practical, devoted to the problem of predicting the development of fires. The works of D.L. Laikhtman, A.S. Gavrilov, and P.M. Matveev were accepted as the main ones. In addition to analyzing these literary sources, the authors applied statistical methods of information processing and used the possibilities of mathematical modeling.
Results. The generally accepted elliptical shape of the contour of a ground forest fire in the R. Rothermel model has been interpreted. Its disadvantages for predicting spot and intense crown fires have been demonstrated. The introduction of parameters such as relative humidity, terrain slope, surface roughness or viscosity, and features of the burning substance into the equation has been evaluated. The types of convection typical of spot and intense crown fires have been indicated: internal (thermal) and external (mechanical). The decision not to consider near-surface turbulence has been justified. To account for surface air layer turbulence, the authors have relied on the concepts of instability and corresponding physical laws. As a result, the basic formula of the R. Rothermel model was supplemented with a second layer so that it was possible to predict the development of a fire from a ground one to an intense crown fire. The dimensionless parameter of 0.397 was replaced by turbulence coefficient kz. This indicator was introduced into the corrected R. Rothermel equation and supplemented with the average Richardson number, which showed the relationship between temperature and the diffusion rate in neighboring layers. From these components, an updated formula has been developed. The results of simulations for typical cases of convective turbulence and fires, with and without turbulence, were presented in tables. Based on the summary data, we could conclude that the model developed within the scope of this work was adequate.
Discussion and Conclusion. When refining the semi-empirical R. Rothermel model for an unsteady surface layer, the introduction of a turbulence coefficient is justified. In addition, it is shown that it is necessary to supplement the single-layer model with second-level formulas characterizing the development of a fire in an unsteady surface layer. The adjusted model should more effectively predict the parameters of spot and intense crown fires. Further refinements of equations for semi-empirical forest fire models are promising, and it is advisable to continue research in this area.
Keywords
For citations:
Andreeva E.S., Sergeeva G.A., Bogdanova I.V. Refinement of the Ground Forest Fire Model Taking into Account Convective Turbulence. Safety of Technogenic and Natural Systems. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF
Introduction. According to the United Nations, the number of severe forest fires is expected to increase by 50% by the end of the 21st century. In 2003, fires in Siberia, Russia, destroyed approximately 22 million hectares of forest ecosystems. In 2004, 2.6 million hectares of forest were affected in Alaska, USA. In 2010, 1.5 million hectares of forest ecosystems were destroyed in Bolivia. In Canada, 0.7 million hectares were lost in 2011, and 3.4 million hectares in 2014. In 2020, wildfires destroyed more than 16.8 million hectares of forest in Australia. The economic damage amounts to billions of dollars.
The frequency of forest fires and the damage they cause raise questions about how to adequately model the risks of their occurrence. This includes forecasting the development of emergencies and developing measures to minimize losses. The construction of model equations assumes that a fire will occur on a specific area during a certain time period. It is also necessary to estimate the possible duration of the fire, which depends on a number of factors that can be difficult to determine [1].
Semi-empirical models allow for the selection and refinement of parameters for effective fire prediction in forest ecosystems. These models are based on the principles of mass, energy, and momentum conservation, and they assume that the model equations can be written in a simplified form. The corresponding coefficients or empirical parameters are obtained as a result of observations or experiments [2]. These models spread in the middle of the 20th century and were mainly used to predict grass-root fire dynamics. They usually take into account various parameters related to the combustibility of forest materials, including the initial condition of the forest stand and terrain features.
Meteorological conditions, particularly wind, play a significant role in the occurrence and spread of forest fires. The combustibility of forest floor materials and terrain slopes, which are taken into account, for example, in Richard Rothermell's model [1-3], are of secondary importance. The aim of this research is to refine the mathematical model of the spread of forest fires. This will allow for better emergency response and quicker, more effective action. Timely action and appropriate measures can help reduce losses associated with forest fires.
Materials and Methods. The study is based on an analysis of works on the surface layer instability by D.L. Laikhtman, the structure of the boundary layer by A.S. Gavrilov et al. [4][5], on the detection of forest fires and their likelihood of becoming intense by P.M. Matveev et al.
The authors also used literary, analytical-statistical, and analytical-graphical methods as well as mathematical modeling.
For this study, problems of mathematical modeling in forest fire prediction were analyzed. The almost insurmountable difficulties in calculations for the most dangerous wildfires were noted [6–8], which were caused by unknown physical characteristics of heat redistribution and the amount of air movement, factors that determined fire parameters.
Therefore, it should be noted that mathematical models do not represent the transformation of spot fires into intense crown fires [9]. In the 1970s, P.M. Matveev established that a fire became a spot one if the intensity of convective flows was sufficient to raise and transport burning particles. At the same time, their burning time should be sufficient to set fire to objects far from the hearth: forest floor, ground vegetation, stands of trees, etc.
In 1964, N.P. Kurbatsky proposed the first model of heat and mass transfer. In it, the burnout area was estimated by the surface air velocity, like most fire propagation models. In 2018, a group of authors proposed a modern version of heat and mass transfer model for predicting fire spotting, taking into account the challenges of writing equations and still not fully solving the problem [9].
As shown in [1–3], spotting is characteristic of any crown fire when the wind increases. However, from the point of view of the ground layer physics, a strong ground flow (wind) will contribute to the ignition and spread of fire in its first stage. At the second stage, both types of convection develop:
- internal (generated by fire, own, thermal, with unstable ground layer air);
- external (created by air-mass conditions, the ground flow velocity loses its significance and prevents the transformation of a surface fire into a spot, crown one).
Gavrilov A.S., Mkhanna A.I., Kharchenko E.V. in the article “Verification of the model of atmospheric boundary layer applied to the problem prediction of air pollution from forest fires” emphasized the need to take into account the proportion of turbulent heat influx in an unstable surface layer with developed thermal turbulence [4]. It was found that even with a very insignificant heat flow q = 0.003 W/m² in surface conditions, the intensity of the turbulent heat influx increased significantly — in 35 minutes from 0 to +10.2°С.
Thus, the role of convection is obvious, especially an internal thermal one [4–5]. This factor should be taken into account when constructing mathematical models of the transformation of spot forest fires into crown fires.
Results. The R. Rothermel model [1][6] is based on empirical material and allows us to efficiently calculate the parameters of a surface forest fire (Fig. 1).
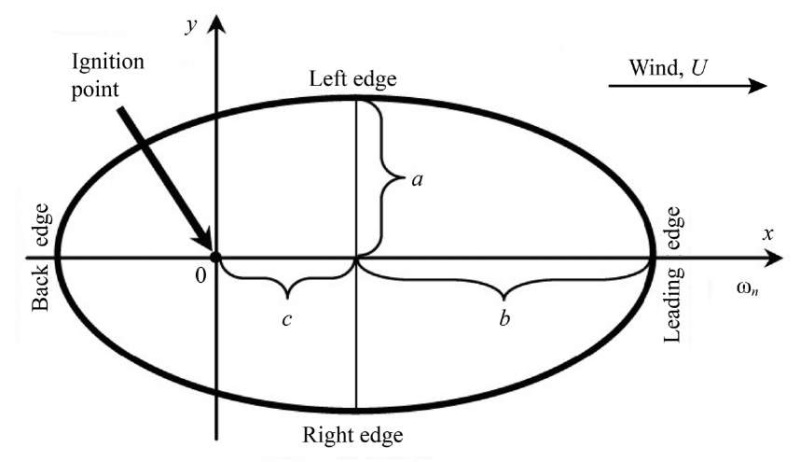
Fig. 1. The generally accepted elliptical shape of the contour of a surface forest fire
To predict the behavior of a forest fire, the ellipse parameters are calculated: a, b and с (formulae 1–3). In this case, the main computational characteristic of the model is the rate of spread of the forest fire, ωn (m/s), which is determined by (4) [1].
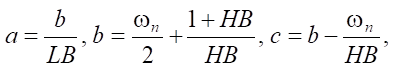 (1)
(1)
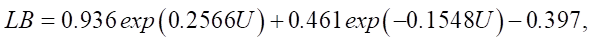 (2)
(2)
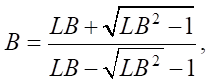 (3)
(3)
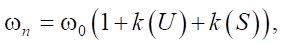 (4)
(4)
where a — segment of the ellipse (height); b — segment of the ellipse (the length in the frontal area of the fire); c — segment of the ellipse (the length of the burnt-out area); LB — width of the ellipse segment b; HB — height of the ellipse segment b; U — flow (wind) velocity, m/s; ωn — speed of forest fire advance, m/min; ω0 — density of the formation of combustible substances, kg/m³; k(U) — size of the particles of vegetative burnt matter, m²; k(S) — rate of complete vegetation burnout, m/min.
The authors believe that this model is not suitable for predicting spot and intense crown fires, as it practically does not take into account meteorological parameters except for the speed of surface flow (wind) [7–8]. In this regard, main predictive equation (2) should be clarified by incorporating additional parameters. Thus, M.A. Sofronov, in 1967, proposed taking into account not only wind speed but also relative humidity, considering its daily fluctuations, and the slope of the terrain and surface roughness or viscosity when assessing the spread rate of surface fires [9–11].
If a crown fire has evolved from a surface one, the rate of fire propagation should be calculated at two levels: near-surface (0–1 m) and surface (1–2 m) [12]. In the near-surface layer, it is more important to take into account the properties of the burning substance, including its density and quantity (see formula 4). In the surface layer (the second level of the model), parameters such as air temperature and humidity, vertical and horizontal flow rates are more significant:
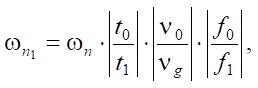 (5)
(5)
where ωn1 — fire advance rate in the surface layer, m/min; ωn — fire advance rate in the near-surface layer, m/min, from formula (4); t0 — air temperature in the near-surface layer, °С; t1 — air temperature in the surface layer at an altitude of 1–2 m, °С; v0 — velocity of the air flow in the near-surface layer, m/sec; vg — horizontal component of the air flow velocity, m/sec; f0 — relative air humidity in the near-surface air layer, %; f1 — relative air humidity in the surface layer at a height of 1–2 m.
With the presence of a spot and intense wildfire, both internal (thermal) and external (mechanical) convection occur. Turbulence causes particles to scatter upwards and away from the source, which can significantly alter the parameters a, b, and c.
The authors note that it is pointless to take turbulence into account in the near-surface layer (0–1 m), since it is extinguished by the surface layer of forest litter or soil. To account for the turbulence of the surface air layers, one should be guided by the concepts of nonstationarity and physical patterns of the surface air layer:
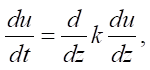 (6)
(6)
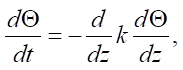 (7)
(7)
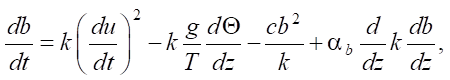 (8)
(8)
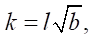 (9)
(9)
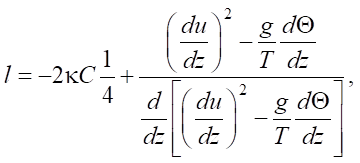 (10)
(10)
where u — air flow velocity, m/s; t — air temperature, °С; z — height, m; Θ — heat inflow, J/s‧m²·kg; b — energy of turbulence, J/kg; g — acceleration of gravity, m/s²; l — scale of turbulence, m; k — turbulence coefficient, m/s; c — D.L. Laichtman constant (~0.046); αb — D.L. Laichtman constant calculated by dimensional analysis (0.73); κ — Karman constant calculated to solve this problem (~0.397).
Based on D.L. Laichtman's ideas about the physical laws of an unsteady surface layer of air, we can conclude about the role of turbulent motions in the distribution of heat, energy, and air particles. In the case of diffusion of matter and energy during heating and transformation of the surface soil layer under fire conditions [13–15], modeling is based on the theory of gradient transfer. k is coefficient of turbulent diffusion. kz is value of diffusion transfer in the vertical plane. Horizontal components of the turbulence coefficient will be negligible due to the surface roughness and the friction force action. To simplify the model equation, we can use the M.I. Budyko equation to calculate vertical diffusion coefficient kz at a unit level
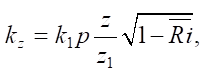 (11)
(11)
where kz — vertical diffusion coefficient, m/s; k1p — kz value at a unit height of z1 and under equilibrium conditions, at a height of 1 m, is 0.1–0.2 m/s; 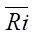 — average Richardson number with respect to the boundary layer, a dimensionless indicator:
— average Richardson number with respect to the boundary layer, a dimensionless indicator:
 (12)
(12)
where T — air temperature, °С; Ta — temperature in the absolute scale, K; g — acceleration of gravity (9.8 m/s²).
The authors propose to supplement initial formula (2) of the R. Rothermel model to clarify the development of a fire from a surface one to an intense crown one (second layer of the model), calculating the rate of fire advance ωn1 in the surface layer according to formula (5). In this case, equation (2) is supplemented by an expression for calculating turbulence coefficient kz and replaced by a dimensionless indicator 0.397, because the latter acts as a parameter that reduces the segment width of ellipse a. According to the authors of this work, taking into account intense convection and subsequent turbulence can help to adjust the width of segment a with greater accuracy in relation to real-world conditions. Then formula (2) can be represented by:
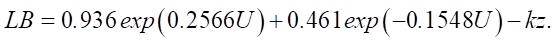 (13)
(13)
Taking into account expressions (11) and (12), we obtain the final:
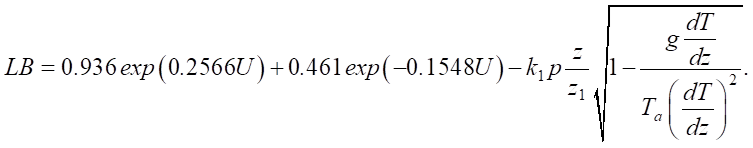 (14)
(14)
Table 1 shows the results of testing equation (14) and modeling typical cases of convective turbulence.
Table 1
Some Results of Modeling Fire Parameters with and Without Turbulence [16] for an Unsteady Surface Layer
|
No. |
Characteristic |
U, m/s |
kz, m/s |
LB |
HB |
a |
b |
c |
|
1 |
Weak |
4.000 |
– |
2.470 |
22.521 |
0.521 |
1.290 |
1.268 |
|
2 |
Weak |
4.000 |
0.500 |
2.370 |
19.640 |
0.552 |
1.301 |
1.276 |
|
3 |
Moderate |
8.000 |
– |
7.001 |
139.001 |
0.220 |
1.507 |
1.500 |
|
4 |
Moderate |
8.000 |
2.000 |
5.400 |
107.002 |
0.281 |
1.509 |
1.500 |
|
5 |
Strong |
12.000 |
– |
11.610 |
579.501 |
0.170 |
2.001 |
1.997 |
|
6 |
Strong |
12.000 |
5.000 |
7.010 |
199.290 |
0.290 |
2.005 |
1.995 |
Discussion and Conclusion. The combustion model under conditions of an unsteady surface layer was considered. The values of segment a of the elliptical fire edge, taking into account refined expression (14), were compared with the classical R. Rothermel formula [16]. An analysis of the simulation results with the turbulence coefficient (Table 1) revealed the largest deviations of these values. At the same time, no significant differences in the parameters of ellipse b and c were found, which may confirm the expediency of the proposed refinement.
Adequacy of the obtained values of ellipse segment a is determined by the Student's criterion (two-sample t-criterion). For this purpose, the calculated values of ellipse segment a in the semi-empirical R. Rothermel model and in equation (14) proposed by the authors were compared. Table 2 provides the test results. The calculated value of the Student's t-test is much less than the critical (tabular) value: 0.609 < 2.776. This proves the statistical convergence of the calculation results in the refined model represented by expression (14).
Table 2
Comparison Results of the Refined Version of the Model Containing the Turbulence Parameter with the Classical Equation of the r. Rothermel Model
|
No. |
Mean value |
Variance |
Degree of freedom |
Combined variance |
Value of t-criterion |
|
|
calculated |
critical* |
|||||
|
1 |
0.374 |
0.016 |
4 |
0.02 |
0.609 |
2.776 |
|
2 |
0.304 |
0.024 |
4 |
|||
|
*With 95% confidence. |
||||||
Note No. 1 corresponds to calculations using equation (14), which takes turbulence into account. No. 2 corresponds to the classical expression of the Rothermel model, without taking turbulence into consideration.
Thus, the introduction of expression (14) is justified for an unsteady surface layer (the second layer of the model) and makes it possible to significantly adjust the size of ellipse segment a, taking into account internal and external vertical convective flows that form turbulence of the surface layer and transform a surface forest fire into an intense crown one.
The adjusted model allows for more efficient calculation of the parameters of spot and intense crown fires within forest ecosystems. Further refinement of the equations for semi-empirical forest fire models is promising. Research in this area should continue.
References
1. Anoikin RK. Analysis of Mathematical Models Used for Forest Ground Fires Forecasting. Tekhnologii Grazhdanskoi Bezopasnosti. 2020;17(2(64)):58–60. (In Russ.) https://doi.org/10.54234/CST.19968493.2020.17.2.64.10.58
2. Кулешов А.А., Мышецкая Е.Е. Математическое моделирование лесных пожаров с применением многопроцессорных ЭВМ. Математическое моделирование. 2008;20(11):28–34. Kuleshov AA, Myshetskaya EE. Mathematical Modeling of Forest Fires Using Supercomputers. Matematicheskoe modelirovanie. 2008;20(11):28–34. (In Russ.)
3. Grishin AM, Pugacheva PV. Analysis of Impact of Forest and Steppe Fires on Cities Andvillages and the New Determinate and Probability Model for Prediction of Firedangerous in Villages and Cities. Tomsk State University Journal of Mathematics and Mechanics. 2009;(3(7)):99–108. (In Russ.) URL: https://www.mathnet.ru/rus/vtgu/y2009/i3/p99 (accessed: 01.09.2024).
4. Gavrilov AS, Mhanna A, Кharchenko EV. Verification of the Model of Atmospheric Boundary Layer Applied to the Problem Prediction of Air Pollution from Forest Fires. Proceedings of the Russian State Hydrometeorological University. 2013;(32):119–129. (In Russ.) URL: https://www.rshu.ru/university/notes/archive/issue32/uz32-119-129.pdf (accessed: 01.09.2024).
5. Andreeva ES. The Possibilities of Using the Minimax Method to Diagnose the State of the Atmosphere. Journal of Atmospheric Science Research. 2022;6(2):42–49. https://doi.org/10.30564/jasr.v6i2.5519
6. Abannikov VN, Seroukhova OS, Mkhanna AIN, Podgaiskii EV. Assessing the Impact of Agrometeorological Conditions on the Yield of Grain and Leguminous Crops in European Russia. IOP Conference Series: Earth and Environmental Science. 2022;1010:012033. http://doi.org/10.1088/1755-1315/1010/1/012033
7. Denisov OV, Pleshko MS, Ponomareva IA, Merenyashev VE. Scale Factor Management in the Studies of Affine Models of Shockproof Garment Elements. E3S Web of Conferences. 2018;33:03068. https://doi.org/10.1051/e3sconf/20183303068
8. Puzach S, Le TA, Nguyen TH. Fire Hazard from Spotting Ignition at Crown Fires for Power Engineering Facilities. Fires and Emergencies: Prevention, Elimination. 2018;(2):64–70. (In Russ.) https://doi.org/10.25257/FE.2018.2.64-70
9. Kuleshov AA, Myshetskaya EE, Yakush SE. Numerical Simulation of Forest Fire Spread Based on Modifired 2D Model. Matematicheskoe modelirovanie. 2016;28(12):20–32. (In Russ.)
10. Denisov OV, Bulygin YI, Ponomarev AE, Ponomareva IA, Lebedeva VV. Innovative Solutions Shockproof Protection in Occupations Associated with an Increased Risk of Injury. IOP Conference Series: Earth and Environmental Science. 2017;50:012044. https://doi.org/10.1088/1755-1315/50/1/012044
11. Denisov O, Andreeva E. An Innovative Approach to the Elimination of Combustion Foci at MSW Landfills (on the Example of the Rostov Region). E3S Web of Conferences. 2021;273:04006. https://doi.org/10.1051/e3sconf/202127304006
12. Karlin LN, Vankevich RE, Tumanovskaya SM, Andreeva ES, Efimova YuV, Khaimina OV, et al. Hydrometeorological Risks. Saint Petersburg: Russian State Hydrometeorological University; 2008. 282 p. (In Russ.)
13. Martynov A, Grekov V, Popova O. Measuring Tool Kit for Express Analysis of Intumescent Fire Protection at a Construction Facility. Fires and Emergencies: Prevention, Elimination. 2021;(3):61–68. (In Russ.) https://doi.org/10.25257/FE.2021.3.61-68
14. Bogdanova I, Dymnikova O, Loskutnikova I. Analysis of the Noise Load from the Manufacturing Enterprise on the Territory of Residential Buildings Based on Complex Mathematical Model. IOP Conference Series: Materials Science and Engineering. 2020;1001:012119. https://doi.org/10.1088/1757-899X/1001/1/012119
15. Adamyan VL, Sergeeva GA, Seferyan LA, Gorlova NYu. Development of Technological Measures to Ensure the Safety of Production Facilities in Petrochemical Industry. IOP Conference Series: Materials Science and Engineering. 2021;1083:012050. https://doi.org/10.1088/1757-899X/1083/1/012050
16. Barovik DV, Taranchuk VB. Algorithmic Foundations of Constructing a Computer Model for Predicting the Spread of Forest Fires. Vestnik Polotskogo gosudarstvennogo universiteta. Seriya C. Fundamental'nye nauki. 2011;12:51–56. (In Russ.)
About the Authors
E. S. AndreevaRussian Federation
Elena S. Andreeva, Dr. Sci. (Geogr.), Associate Professor, Professor of the Department of Life Safety and Environmental Protection
1, Gagarin Sq., Rostov-on-Don, 344003
G. A. Sergeeva
Russian Federation
Galina A. Sergeeva, Cand. Sci. (Geogr.), Associate Professor of the Department of Life Safety and Environmental Protection
1, Gagarin Sq., Rostov-on-Don, 344003
I. V. Bogdanova
Russian Federation
Irina V. Bogdanova, Cand. Sci. (Eng.), Associate Professor of the Department of Life Safety and Environmental Protection
1, Gagarin Sq., Rostov-on-Don, 344003
Review
For citations:
Andreeva E.S., Sergeeva G.A., Bogdanova I.V. Refinement of the Ground Forest Fire Model Taking into Account Convective Turbulence. Safety of Technogenic and Natural Systems. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF








































