Перейти к:
Уточнение модели низового лесного пожара с учетом конвективной турбулентности
https://doi.org/10.23947/2541-9129-2025-9-1-14-21
EDN: XCYIOF
Аннотация
Введение. В научной литературе довольно активно обсуждается тема математического моделирования развития лесных пожаров для прогнозов скорости их распространения и площади, которую они охватят. С точки зрения процессов турбулентности оцениваются потенциальная высота и отклонение столбов огня, дыма, горячего воздуха, разброс частиц горения и рациональные направления гашения огня. Однако известные модели не дают четкого представления о том, как срабатывает турбулентность при переходе пожара с приповерхностного слоя на нестационарный приземный и выше. Иными словами, сложно просчитать переход низового пожара в его более опасную интенсивную форму. Восполнение этого недостатка — актуальная научная и прикладная задача. Цель данной работы — уточнить уравнения математических моделей распространения низовых лесных пожаров для лучшего контроля за этими инцидентами, что в итоге будет способствовать уменьшению рисков и сокращению ущерба от них.
Материалы и методы. Для достижения цели исследования были изучены труды, охватывающие разные подходы, как теоретические, так и прикладныепрогнозирования развития пожаров. В качестве основных приняты работы Д.Л. Лайхтмана, А.С. Гаврилова, П.М. Матвеева. Кроме анализа этих литературных источников, авторы применяли статистические методы обработки информации и использовали возможности математического моделирования.
Результаты исследования. Интерпретирована общепринятая эллиптическая форма контура низового лесного пожара в модели Р. Ротермела. Показаны ее недостатки для прогнозирования пятнистых и интенсивных верховых пожаров. Оценено введение в уравнение таких параметров, как относительная влажность воздуха, уклон местности, шероховатость или вязкость поверхности, особенности горящего вещества. Обозначены виды конвекций, характерных для пятнистого и интенсивного верхового пожара: внутренняя (термическая) и внешняя (механическая). Обоснован отказ от учета приповерхностной турбулентности. Для рассмотрения турбулентности приземных слоев воздуха авторы руководствовались представлениями о нестационарности и соответствующих физических закономерностях. В итоге базовая формула модели Р. Ротермела была дополнена вторым слоем, чтобы можно было прогнозировать развитие пожара от низового к интенсивному верховому. Безразмерный параметр 0,397 заменен коэффициентом турбулентности kz, этот показатель внесен в откорректированное равенство Р. Ротермела и дополнен средним числом Ричардсона, которое показывает зависимость между температурой и скоростью диффузии в соседних слоях. Из этих составляющих была сформирована обновленная формула. В виде таблиц представлены результаты моделирования характерных случаев развития конвективной турбулентности и пожаров (с учетом и без учета турбулентности). Сводные данные позволяют говорить об адекватности модели, созданной в рамках представленной работы.
Обсуждение и заключение. При уточнении полуэмпирической модели Р. Ротермела для нестационарного приземного слоя обосновано введение коэффициента турбулентности. Кроме того, показана необходимость дополнения однослойной модели формулами второго уровня, характеризующими развитие пожара в нестационарном приземном слое. Откорректированная модель должна более эффективно прогнозировать параметры пятнистых и интенсивных верховых пожаров. Перспективны дальнейшие уточнения уравнений полуэмпирических моделей лесных пожаров. Целесообразно продолжить исследования в этом направлении.
Ключевые слова
Для цитирования:
Андреева Е.С., Сергеева Г.А., Богданова И.В. Уточнение модели низового лесного пожара с учетом конвективной турбулентности. Безопасность техногенных и природных систем. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF
For citation:
Andreeva E.S., Sergeeva G.A., Bogdanova I.V. Refinement of the Ground Forest Fire Model Taking into Account Convective Turbulence. Safety of Technogenic and Natural Systems. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF
Введение. По данным ООН, к концу XXI века количество интенсивных лесных пожаров возрастет на 50 %. В 2003 году пожары в Сибири (Российская Федерация) уничтожили около 22 млн га лесных экосистем. В 2004 году на Аляске (США) пострадало 2,6 млн га леса. В 2010 году в Боливии уничтожено 1,5 млн га лесных экосистем. В Канаде в 2011 году погибло 0,7 млн га, а в 2014 году — 3,4 млн га. В 2020 году в Австралии лесные пожары уничтожили более 16,8 млн га леса. Экономический ущерб исчисляется миллиардами долларов.
Частота лесных пожаров и ущерб от них ставят вопросы об адекватном моделировании соответствующих рисков их возникновения, о прогнозировании развития чрезвычайной ситуации и разработке мер по снижению потерь. Построение модельных уравнений предполагает, что горение происходит на определенной площади в течение конкретного времени. Необходимо также рассчитать возможную длительность пожара, которая зависит от комплекса факторов, зачастую трудно определяемых [1].
Полуэмпирические модели позволяют подбирать и уточнять параметры для эффективного прогноза пожаров в лесных экосистемах. Такие формулы базируются на законах сохранения массы, энергии и движения. Они предполагают запись модельных уравнений в упрощенном виде, а соответствующие коэффициенты или эмпирические параметры можно получить в результате наблюдений или экспериментов [2]. Рассмотренные модели распространились в середине XX века и использовались в основном для прогноза динамики низовых пожаров. Обычно в них учитываются параметры горючести лесного материала, в том числе исходное состояние древостоя и рельеф местности.
Определяющими факторами возникновения и развития лесного пожара будут метеорологические условия, особенно ветер. Горючесть материла лесной подстилки или уклоны местности, учитываемые, например, в модели Ричарда Ротермела [1–3], имеют второстепенное значение. Цель данного исследования — уточнить математическую модель распространения лесных пожаров. Она позволит точнее прогнозировать развитие чрезвычайной ситуации и, соответственно, более оперативно и адекватно реагировать на нее. Своевременная реакция и принимаемые меры должны сократить потери, связанные с пожарами.
Материалы и методы. Исследование базируется на анализе трудов о нестационарности приземного слоя Д.Л. Лайхтмана, о строении пограничного слоя А.С. Гаврилова и др. [4][5], о пятнистости лесных пожаров и вероятности их преобразований в интенсивные верховые П.М. Матвеева и др.
Авторы задействовали также литературные, аналитико-статистические, аналитико-графические методы, математическое моделирование.
Для данного исследования проанализированы проблемы математического моделирования при прогнозировании лесных пожаров. Отмечены практически непреодолимые сложности расчетов по наиболее опасным верховым пожарам [6–8], которые обусловлены неизвестными физическими характеристиками перераспределения тепла и количества движения воздуха — факторами, определяющими параметры пожара.
Итак, следует отметить, что в математических моделях не представлена трансформация пятнистых возгораний в интенсивный верховой пожар [9]. В 70-е годы XX века П.М. Матвеев установил, что пожар становится пятнистым, если интенсивности конвективных потоков хватает для поднятия и переноса горящих частиц. При этом времени их горения должно быть достаточно, чтобы поджечь удаленные от очага объекты: лесную подстилку, надпочвенный покров, древостой и пр.
В 1964 году Н.П. Курбатский предложил первую модель тепломассообмена. В ней площадь выгора оценивалась по скорости приземного воздуха, как и большинство моделей распространения огня. В 2018 году группа авторов предложила современную версию модели тепломассообмена для прогноза пятнистости возгораний, отметив сложности при составлении уравнений и не решив проблему до конца [9].
Как показано в [1–3], пятнистость свойственна любому верховому пожару при усилении ветра. Однако с точки зрения физики приземного слоя сильный приземный поток (ветер) будет способствовать возгоранию и распространению огня на первой стадии пожара. На второй стадии развиваются оба вида конвекции:
- внутренняя (порождаемая пожаром, собственная, тепловая, с неустойчивым приземным слоем воздуха);
- внешняя (создается внутримассовыми условиями, скорость приземного потока утрачивает значение и препятствует трансформации низового пожара в пятнистый, верховой).
Гаврилов А.С., Мханна А.И., Харченко Е.В. в статье «Верификация модели атмосферного пограничного слоя применительно к задачам прогноза загрязнения атмосферы от очагов лесных пожаров» подчеркивают необходимость учета доли турбулентного притока тепла в условиях нестационарного приземного слоя с развитой тепловой турбулентностью [4]. Установлено, что даже при весьма незначительном тепловом потоке, q = 0,003 Вт/м² в приземных условиях, интенсивность турбулентного притока тепла существенно увеличивалась — за 35 минут с 0 до +10,2 °С.
Таким образом, очевидна роль конвекции, особенно тепловой внутренней [4][5]. Этот фактор нужно учитывать при построении математических моделей трансформации пятнистых лесных пожаров в верховые.
Результаты исследования. Модель Р. Ротермела [1][6] базируется на эмпирическом материале и позволяет результативно рассчитывать параметры низового лесного пожара (рис. 1).
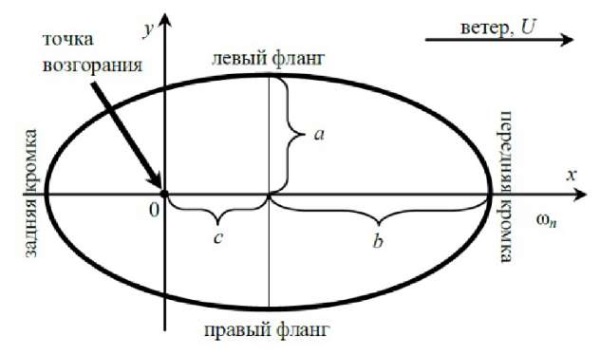
Рис. 1. Общепринятая эллиптическая форма контура низового лесного пожара
Для прогнозирования поведения лесного пожара вычисляются параметры эллипса: a, b и с (формулы 1–3). При этом центральной расчетной характеристикой модели будет скорость продвижения лесного пожара, ωn (м/сек), определяемая по (4) [1].
 (1)
(1)
 (2)
(2)
 (3)
(3)
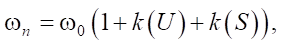 (4)
(4)
где a — отрезок эллипса (высота); b — отрезок эллипса (длина во фронтальной зоне огня); c — отрезок эллипса (длина выгора); LB — ширина отрезка эллипса b; HB — высота отрезка эллипса b; U — скорость потока (ветра), м/сек; ωn — скорость продвижения лесного пожара, м/мин; ω0 — плотность пласта горючих веществ, кг/м³; k(U) — величина частичек вегетативной прогораемой материи, м²; k(S) — скорость полного прогорания растительности, м/мин.
Авторы полагают, что данная модель неприменима для прогнозирования пятнистых и интенсивных верховых пожаров. Кроме того, она практически не учитывает метеорологические параметры за исключением скорости приземного потока (ветра) [7][8]. В этой связи следует уточнить основное прогностическое уравнение (2), включив в него дополнительные параметры. Так, в 1967 году М.А. Софронов предложил при оценке скорости распространения низового пожара учитывать не только скорость ветра, но и относительную влажность воздуха с учетом ее суточных флуктуаций, а также уклон местности, шероховатость или вязкость поверхности [9–11].
Если верховой пожар эволюционировал из низового, скорость распространения огня нужно вычислять на двух уровнях: приповерхностном (0–1 м) и приземном (1–2 м) [12]. В приповерхностном слое важнее учесть характеристики горящего вещества, включая его плотность и количество (см. формулу 4). В приземном слое (второй уровень модели) более важными будут такие параметры, как температура и влажность воздуха, вертикальные и горизонтальные скорости потока:
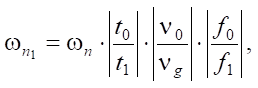 (5)
(5)
где ωn1 — скорость продвижения огня в приземном слое, м/мин; ωn — скорость продвижения пожара в приповерхностном слое, м/мин, из формулы (4); t0 — температура воздуха в приповерхностном слое, °С; t1 — температура воздуха в приземном слое на высоте 1–2 м, °С; v0 — скорость потока воздуха в приповерхностном слое, м/сек; vg — горизонтальная составляющая скорости потока воздуха, м/сек; f0 — относительная влажность воздуха в приповерхностном слое воздуха, %; f1 — относительная влажность воздуха в приземном слое на высоте 1–2 м.
При пятнистом и интенсивном верховом пожаре развивается внутренняя (термическая) и внешняя (механическая) конвекция. Турбулентность «разбрасывает» частицы вверх и в стороны от очага, что может существенно изменить параметры a, b и c.
Авторы отмечают, что в приповерхностном слое (0–1 м) бессмысленно учитывать турбулентность, так как она гасится поверхностным слоем лесной подстилки или почвы. Для учета турбулентности приземных слоев воздуха следует руководствоваться представлениями о нестационарности и физических закономерностях приземного слоя воздуха:
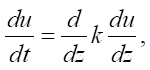 (6)
(6)
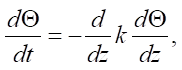 (7)
(7)
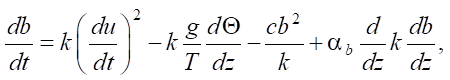 (8)
(8)
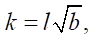 (9)
(9)
 (10)
(10)
где u — скорость потока воздуха, м/сек; t — температура воздуха, °С; z — высота, м; Θ — приток тепла, Дж/с м²·кг; b — энергия турбулентности, Дж/кг; g — ускорение свободного падения, м/сек²; l — масштаб турбулентности, м; k — коэффициент турбулентности, м/сек; c — постоянная Д.Л. Лайхтмана (~0,046); αb — постоянная Д.Л. Лайхтмана, рассчитанная по анализу размерностей (0,73); κ — постоянная Кармана, вычисленная для решения данной задачи (~0,397).
Исходя из представлений Д.Л. Лайхтмана о физических закономерностях нестационарного приземного слоя воздуха, можно сделать вывод о роли турбулентных движений в распределении тепла, энергии, частиц воздуха. В случае диффузии вещества и энергии при нагревании и трансформации поверхностного слоя почвы в условиях пожара [13–15] моделирование основывается на теории градиентного переноса. Коэффициент турбулентной диффузии — k. Значение диффузионного переноса в вертикальной плоскости — kz. Горизонтальные составляющие коэффициента турбулентности будут пренебрежимо малы из-за шероховатости поверхности и действия силы трения. Для упрощения модельного уравнения следует воспользоваться уравнением М.И. Будыко, рассчитывающим коэффициент вертикальной диффузии kz на единичном уровне:
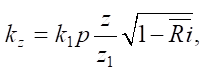 (11)
(11)
где kz — коэффициент вертикальной диффузии, м/сек; k1p — значение kz на единичной высоте z1 и в равновесных условиях, на высоте 1 м составляет 0,1–0,2 м/сек; 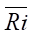 — среднее по пограничному слою число Ричардсона, безразмерный показатель:
— среднее по пограничному слою число Ричардсона, безразмерный показатель:
 (12)
(12)
где T — температура воздуха, °С; Ta — температура в абсолютной шкале, К; g — ускорение свободного падения (9,8 м/сек²).
Авторы предлагают внести дополнения в исходную формулу (2) модели Р. Ротермела для уточнения развития пожара от низового к интенсивному верховому (второй слой модели), рассчитывая скорость продвижения огня ωn1 в приземном слое по формуле (5). При этом уравнение (2) дополняется выражением для расчета коэффициента турбулентности kz и заменяется им безразмерный показатель 0,397, поскольку по смыслу последний выполняет роль параметра, снижающего ширину отрезка эллипса a. По мнению авторов данной работы, учет интенсивной конвекции и последующей турбулентности способен скорректировать ширину отрезка a с большей точностью по отношению к реальным условиям. Тогда формулу (2) можно представить:
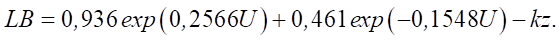 (13)
(13)
С учетом выражений (11) и (12) получим итоговое:
 (14)
(14)
В таблице 1 представлены результаты апробации уравнения (14) и моделирования характерных случаев развития конвективной турбулентности.
Таблица 1
Некоторые результаты моделирования параметров пожаров с учетом и без учета турбулентности [16] для нестационарного приземного слоя
|
№ |
Характеристика |
U, м/сек |
kz, м/сек |
LB |
HB |
a |
b |
c |
|
1 |
Слабый |
4,000 |
– |
2,470 |
22,521 |
0,521 |
1,290 |
1,268 |
|
2 |
Слабый |
4,000 |
0,500 |
2,370 |
19,640 |
0,552 |
1,301 |
1,276 |
|
3 |
Умеренный |
8,000 |
– |
7,001 |
139,001 |
0,220 |
1,507 |
1,500 |
|
4 |
Умеренный |
8,000 |
2,000 |
5,400 |
107,002 |
0,281 |
1,509 |
1,500 |
|
5 |
Сильный |
12,000 |
– |
11,610 |
579,501 |
0,170 |
2,001 |
1,997 |
|
6 |
Сильный |
12,000 |
5,000 |
7,010 |
199,290 |
0,290 |
2,005 |
1,995 |
Обсуждение и заключение. Итак, рассмотрена модель горения в условиях нестационарного приземного слоя. Значения отрезка a эллиптического контура пожара с учетом уточненного выражения (14) сравнивались с классической формулой Р. Ротермела [16]. Анализ результатов моделирования с коэффициентом турбулентности (таблица 1) позволил выявить наибольшие отклонения указанных значений. При этом не обнаружены существенные различия параметров эллипса b и c, что может подтвердить целесообразность предложенного уточнения.
Адекватность полученных значений отрезка a эллипса определена по критерию Стьюдента (двухвыборочный t-критерий). Для этого сравнивались вычисленные значения отрезка эллипса a в полуэмпирической модели Р. Ротермела и в предложенном авторами уравнении (14). Результаты проверки приводятся в таблице 2. Вычисленное значение t-критерия Стьюдента намного меньше критического (табличного): 0,609 < 2,776. Это доказывает статистическую сходимость результатов расчетов в уточненной модели, представленной выражением (14).
Таблица 2
Результаты сравнения уточненного варианта модели, содержащего параметр турбулентности, с классическим уравнением модели Р. Ротермела
|
№ |
Среднее значение |
Дисперсия |
Степени свободы |
Объединенная дисперсия |
Значение t-критерия |
|
|
вычисленное |
критическое* |
|||||
|
1 |
0,374 |
0,016 |
4 |
0,02 |
0,609 |
2,776 |
|
2 |
0,304 |
0,024 |
4 |
|||
|
*При достоверности 95 %. |
||||||
Примечание № 1 соответствует расчетам с применением уравнения (14), учитывающего турбулентность. № 2 соответствует расчетам классического выражения модели Р. Ротермела без учета турбулентности.
Таким образом, введение выражения (14) обосновано для нестационарного приземного слоя (второй слой модели) и позволяет существенно корректировать размеры отрезка a эллипса с учетом внутренних и внешних вертикальных конвективных потоков, которые формируют турбулентность приземного слоя и трансформируют низовой лесной пожар в интенсивный верховой.
Скорректированная модель дает возможность более эффективно рассчитывать параметры пятнистых и интенсивных верховых пожаров в пределах лесных экосистем. Перспективны дальнейшие уточнения уравнений полуэмпирических моделей лесных пожаров. Следует продолжать исследования в этом направлении.
Список литературы
1. Анойкин Р.К. Анализ математических моделей, используемых для прогнозирования низовых лесных пожаров. Технологии гражданской безопасности. 2020;17(2(64)):58–60. https://doi.org/10.54234/CST.19968493.2020.17.2.64.10.58
2. Кулешов А.А., Мышецкая Е.Е. Математическое моделирование лесных пожаров с применением многопроцессорных ЭВМ. Математическое моделирование. 2008;20(11):28–34.
3. Гришин А.М., Пугачева П.В. Анализ действия лесных и степных пожаров на города и поселки и новая детерминированно-вероятностная модель прогноза пожарной опасности в населенных пунктах. Вестник Томского государственного университета. Математика и механика. 2009;(3(7)):99–108. URL: https://www.mathnet.ru/rus/vtgu/y2009/i3/p99 (дата обращения: 01.09.2024).
4. Гаврилов А.С., Мханна А.И.Н., Харченко Е.В. Верификация модели атмосферного пограничного слоя применительно к задачам прогноза загрязнения атмосферы от очагов лесных пожаров. Ученые записки Российского государственного гидрометеорологического университета. 2013;(32):119–129. URL: https://www.rshu.ru/university/notes/archive/issue32/uz32-119-129.pdf (дата обращения: 01.09.2024).
5. Andreeva ES. The Possibilities of Using the Minimax Method to Diagnose the State of the Atmosphere. Journal of Atmospheric Science Research. 2022;6(2):42–49. https://doi.org/10.30564/jasr.v6i2.5519
6. Abannikov VN, Seroukhova OS, Mkhanna AIN, Podgaiskii EV. Assessing the Impact of Agrometeorological Conditions on the Yield of Grain and Leguminous Crops in European Russia. IOP Conference Series: Earth and Environmental Science. 2022;1010:012033. http://doi.org/10.1088/1755-1315/1010/1/012033
7. Denisov OV, Pleshko MS, Ponomareva IA, Merenyashev VE. Scale Factor Management in the Studies of Affine Models of Shockproof Garment Elements. E3S Web of Conferences. 2018;33:03068. https://doi.org/10.1051/e3sconf/20183303068
8. Пузач С.В. Ле Ань Туан, Нгуен Тхань Хай. Пожарная опасность пятнистого возгорания при верховом лесном пожаре для объектов энергетики. Пожары и чрезвычайные ситуации: предотвращение и ликвидация. 2018;(2):64–70. https://doi.org/10.25257/FE.2018.2.64-70
9. Кулешов А.А., Мышецкая Е.Е., Якуш С.Е. Моделирование распространения лесных пожаров на основе модифицированной двумерной модели. Математическое моделирование. 2016;28(12):20–32.
10. Denisov OV, Bulygin YI, Ponomarev AE, Ponomareva IA, Lebedeva VV. Innovative Solutions Shockproof Protection in Occupations Associated with an Increased Risk of Injury. IOP Conference Series: Earth and Environmental Science. 2017;50:012044. https://doi.org/10.1088/1755-1315/50/1/012044
11. Denisov O, Andreeva E. An Innovative Approach to the Elimination of Combustion Foci at MSW Landfills (on the Example of the Rostov Region). E3S Web of Conferences. 2021;273:04006. https://doi.org/10.1051/e3sconf/202127304006
12. Карлин Л.Н., Ванкевич Р.Е., Тумановская С.М., Андреева Е.С., Ефимова Ю.В., Хаймина О.В. и др. Гидрометеорологические риски. Санкт-Петербург: Российский государственный гидрометеорологический университет; 2008. 282 с.
13. Мартынов А.В., Греков В.В., Попова О.В. Комплект средств измерений для экспресс-анализа интумесцентной огнезащиты на строительном объекте. Пожары и чрезвычайные ситуации: предотвращение, ликвидация. 2021;(3):61–68. https://doi.org/10.25257/FE.2021.3.61-68
14. Bogdanova I, Dymnikova O, Loskutnikova I. Analysis of the Noise Load from the Manufacturing Enterprise on the Territory of Residential Buildings Based on Complex Mathematical Model. IOP Conference Series: Materials Science and Engineering. 2020;1001:012119. https://doi.org/10.1088/1757-899X/1001/1/012119
15. Adamyan VL, Sergeeva GA, Seferyan LA, Gorlova NYu. Development of Technological Measures to Ensure the Safety of Production Facilities in Petrochemical Industry. IOP Conference Series: Materials Science and Engineering. 2021;1083:012050. https://doi.org/10.1088/1757-899X/1083/1/012050
16. Баровик Д.В., Таранчук В.Б. Алгоритмические основы построения компьютерной модели прогноза распространения лесных пожаров. Вестник Полоцкого государственного университета. Фундаментальные науки. 2011;12:51–56.
Об авторах
Е. С. АндрееваРоссия
Елена Сергеевна Андреева, доктор географических наук, доцент, профессор кафедры безопасности жизнедеятельности и защиты окружающей среды
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Г. А. Сергеева
Россия
Галина Александровна Сергеева, кандидат географических наук, доцент кафедры безопасности жизнедеятельности и защиты окружающей среды
344003, г. Ростов-на-Дону, пл. Гагарина, 1
И. В. Богданова
Россия
Ирина Виссарионовна Богданова, кандидат технических наук, доцент кафедры безопасности жизнедеятельности и защиты окружающей среды
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Андреева Е.С., Сергеева Г.А., Богданова И.В. Уточнение модели низового лесного пожара с учетом конвективной турбулентности. Безопасность техногенных и природных систем. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF
For citation:
Andreeva E.S., Sergeeva G.A., Bogdanova I.V. Refinement of the Ground Forest Fire Model Taking into Account Convective Turbulence. Safety of Technogenic and Natural Systems. 2025;9(1):14-21. https://doi.org/10.23947/2541-9129-2025-9-1-14-21. EDN: XCYIOF








































