Перейти к:
Метод вероятностной сетки для закона Фишера – Типпета
https://doi.org/10.23947/2541-9129-2025-9-2-146-157
EDN: TCVEAL
Аннотация
Введение. Оценка параметров вероятностных законов распределения с использованием вероятностных сеток находит широкое применение на практике, особенно в современных программных комплексах. Такой подход активно используется для статистического анализа, где результаты вычислений представляются в виде вероятностного графика, что даёт возможность оценить соответствие набора данных предполагаемой вероятностной модели и выявить выбросы. В контексте вероятностной оценки нагруженности элементов машин и конструкций некоторые авторы предлагают применять закон Фишера – Типпета. Этот закон характеризуется функцией распределения, которая содержит три параметра и ориентирована на максимум, что обеспечивает гибкость в описании статистических данных и позволяет получать оценку максимального значения в контексте нагруженности. Тем не менее, в существующей литературе недостаточно обоснованы графическое представление результатов вычислений и методика оценки параметров, в том числе и с использованием метода вероятностной сетки, что ограничивает практическое применение закона Фишера – Типпета. Таким образом, основная цель данного исследования заключается в обосновании и разработке методики оценки параметров закона Фишера – Типпета с использованием метода вероятностной сетки.
Материалы и методы. В качестве материалов рассматривались принципы и теоретические основы построения вероятностных сеток, предварительная группировка данных и ранговый метод оценки эмпирической функции распределения. Обосновывались аналитические зависимости для построения вероятностной сетки и оценки параметров закона Фишера – Типпета. Использовались метод математического моделирования и сравнительный анализ. Для моделирования задействовали программный комплекс «Матлаб 8.6». Данные обобщали в табличном формате и визуализировали в виде графиков.
Результаты исследования. Обоснована и показана на примере методика построения вероятностного графика и методика графической оценки параметров закона Фишера – Типпета. Представлены график эмпирической функции распределения и вероятностный график с описанием позиций. Предложена методика построения специальной шкалы для оценки параметра формы, ориентированной на точку отсчета в начале координат. Выполнен сравнительный анализ оценок параметров, полученных графическим и аналитическим методами. Сопоставлялись оценки параметров масштаба, формы и сдвига. Относительная погрешность оценок методом вероятностной сетки не превышает 2 %. Показатель для параметра масштаба — 1,83 %; формы — 0,67 %, сдвига — 0,45 %. Соответствующие итоги аналитической оценки: 4,4 %, 9,33 % и 2,13 %. В данном случае погрешность выше, однако это не значит, что аналитический метод менее точен.
Обсуждение и заключение. Показана адекватность предложенной методики графической оценки параметров закона Фишера – Типпета методом вероятностной сетки. Ее можно применять, например, в программных комплексах или пользовательских приложениях. Специальная шкала для графической оценки параметра формы также подходит для оценки параметра формы закона Вейбулла. Полученные аналитические зависимости, положения методики и графический материал можно использовать при разработке соответствующего национального стандарта.
Ключевые слова
Для цитирования:
Котесов А.А. Метод вероятностной сетки для закона Фишера – Типпета. Безопасность техногенных и природных систем. 2025;(2):146-157. https://doi.org/10.23947/2541-9129-2025-9-2-146-157. EDN: TCVEAL
For citation:
Kotesov A.A. Probability Grid Method for Fisher-Tippett Law. Safety of Technogenic and Natural Systems. 2025;(2):146-157. https://doi.org/10.23947/2541-9129-2025-9-2-146-157. EDN: TCVEAL
Введение. Графическое представление результатов статистического анализа в виде вероятностных графиков широко применяется в современных программных комплексах, в частности при анализе надежности или выживаемости. Это позволяет оценить параметры закона распределения и идентифицировать выбросы1. Оценка параметров с помощью вероятностных сеток используется наряду с другими известными методами и в некоторых случаях может быть предпочтительнее. Вероятностные графики применяют при обработке результатов ресурсных испытаний2 и составлении контрольных карт в системах управления качеством3. Метод вероятностной сетки позволяет визуально оценить соответствие набора данных предполагаемой модели случайной величины, о чем говорится в работах
Дерябина М.А. [1], Добротина С.А. [2], Шпера В.Л. [3], Буланова Я.И. [4], Аблазовой К.С. [5], Великановой Н.П. [6], Хазановича Г.Ш. [7] и других современных ученых.
Касьянов В.Е. [8] и Котесов А.А. [9] для вероятностной оценки нагруженности элементов машин и конструкций предлагают использовать одну из форм обобщенного распределения экстремальных значений [10] с определенным видом параметризации, которую предлагают называть законом Фишера – Типпета. Данная модель похожа на трехпараметрический закон Вейбулла, но в отличие от него ориентирована на максимальное значение. Закон Фишера – Типпета подходит для оценки показателей надежности совместно с законом Вейбулла, к примеру, при использовании модели отказа нагрузка — прочность [11].
Графическое представление результатов вычислений и методика оценки параметров для данного закона не обоснованы должным образом. В научной литературе и нормативно-технической документации не представлена методика оценки параметров с помощью вероятностной сетки, что ограничивает практическое применение закона Фишера – Типпета. Поэтому основная цель данного исследования заключалась в обосновании и разработке методики оценки параметров закона Фишера – Типпета с использованием метода вероятностной сетки.
Материалы и методы. Оценка параметров распределения с помощью вероятностных графиков основана на группировке данных по интервалам и построении интервального эмпирического распределения независимо от предполагаемого теоретического распределения. Поэтому такие методы часто называют непараметрическими или ранговыми. Вероятностная сетка строится для конкретного закона распределения вероятностей с целью получения линейной зависимости между переменными4. Построение графика предполагает линейную аппроксимацию массива эмпирических точек на вероятностной сетке. Поэтому такой подход считается несколько грубым, но достаточно часто применяется наряду с другими. Метод вероятностной сетки может быть определяющим в случае, когда другие методы несостоятельны. К примеру, при получении оценок параметров методом максимального правдоподобия функция правдоподобия может содержать несколько локальных максимумов. В этом случае оценки параметров могут быть весьма неточными [12].
Для обоснования вероятностной сетки функцию распределения вероятностного закона необходимо привести к линейному виду. Функция распределения закона Фишера – Типпета определяется выражением:
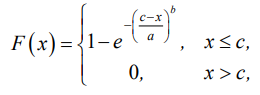 (1)
(1)
где x — значение случайной величины; a, b, c — соответственно параметры масштаба, формы и сдвига распределения.
Преобразуем функцию распределения (1) путем логарифмирования левой и правой части. При условии, что c > х, получим:
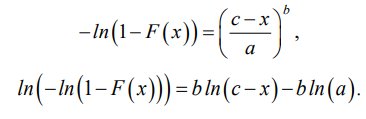 (2)
(2)
Очевидно, что выражение (2) — это линейная функция вида:
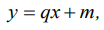 (3)
(3)
где х — переменная функции; q и m — константы.
Сопоставив (2) и (3), получим:
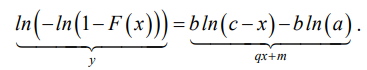
Выражение (2) отличается от аналогичного, обоснованного для закона Вейбулла с тремя параметрами, только правой частью:
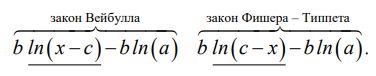
Поэтому для построения вероятностного графика закона Фишера – Типпета целесообразно использовать основные положения ГОСТ 11.008 и ГОСТ 50779.27. Согласно этим стандартам, при графическом анализе статистические данные наносятся на вероятностную сетку, а затем оцениваются параметры распределения. Отметим, что метод вероятностной сетки реализуется как графоаналитическим способом, так и полностью аналитическим. Поэтому для устранения возможной неясности будем называть оценку параметров с помощью метода вероятностной сетки — графической, а оценку методом максимального правдоподобия — аналитической.
Левая часть выражения (2) позволяет определить ординату вероятностной шкалы для оценки параметра масштаба. Предположим, что с – х = а. Подставив это значение в (2), получим:
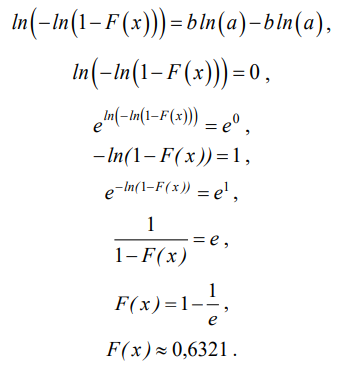 (4)
(4)
Результат (4) позволяет сделать вывод, что абсцисса точки аппроксимирующей прямой с нулевой ординатой будет оценкой параметра масштаба.
По оси абсцисс вероятностного графика может быть использован десятичный логарифм. В этом случае зависимость (2) примет вид:
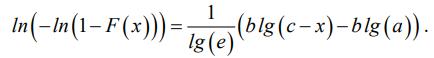
Важный момент при реализации метода вероятностной сетки — предварительная обработка исходных статистических данных, в частности, получение интервального вариационного ряда и оценка значений эмпирической функции распределения. Как правило, для получения эмпирической функции распределения применяется ранговый метод, который базируется на оценке позиции распределения упорядоченных данных с учетом характеристик вариационного ряда (среднего значения, медианы, моды и т. д.). Поэтому для определения ординат точек применяются различные зависимости, в том числе выражения для приближенной оценки [13]. В данном случае выбор будет обусловлен количеством эмпирических данных, предполагаемым теоретическим распределением и видом вероятностного графика. При этом учитывается необходимость адекватного описания крайних членов вариационного ряда [14].
Следует отметить, что некоторые ранее обоснованные подходы к оценке эмпирической функции распределения подвергаются критике, и это может быть предметом отдельного рассмотрения [15].
Результаты исследования. Методом обратных функций выполнено моделирование набора случайных данных без определенного физического смысла, распределенных по закону Фишера – Типпета.
Обратная функция распределения получена аналитически из выражения (1):
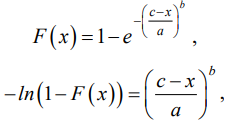
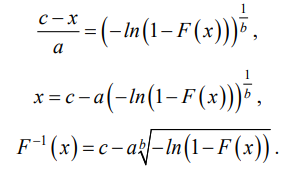 (5)
(5)
Моделирование выполнено с помощью программного комплекса Маtlab 8.6 («Матлаб 8.6», рис. 1) по заданным параметрам закона — a, b, c. Исходные данные для моделирования представлены в таблице 1.
Таблица 1
Исходные данные для моделирования
|
Параметры закона Фишера – Типпета |
Количество значений |
||
|
a |
b |
c |
n |
|
100,00 |
3,00 |
250,00 |
100 |
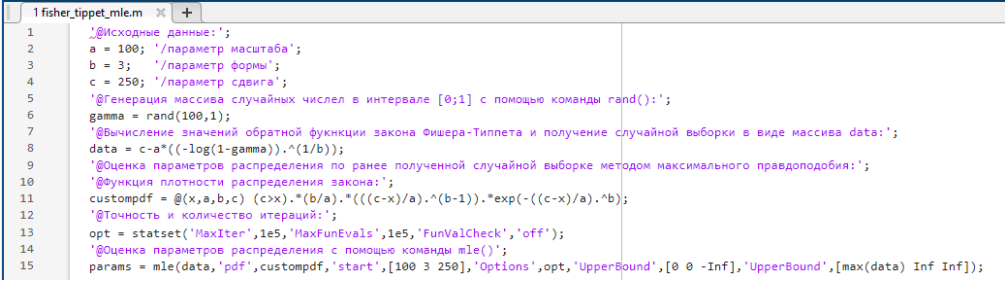
Рис. 1. Моделирование набора случайных данных в Matlab 8.6
Результаты моделирования в виде набора случайных данных xi представлены в таблице 2.
Таблица 2
Набор случайных данных без определенного физического смысла
|
№ |
xi |
|||||||||
|
1 |
201,98 |
222,87 |
182,26 |
183,98 |
133,30 |
114,41 |
204,15 |
157,16 |
169,63 |
217,17 |
|
2 |
124,97 |
100,63 |
138,10 |
112,03 |
185,71 |
160,66 |
169,88 |
123,02 |
192,45 |
179,76 |
|
3 |
143,79 |
97,90 |
118,26 |
208,58 |
152,80 |
95,93 |
179,54 |
214,92 |
155,05 |
132,63 |
|
4 |
140,21 |
199,05 |
140,76 |
179,14 |
200,77 |
189,65 |
178,47 |
117,03 |
152,32 |
174,79 |
|
5 |
148,32 |
164,27 |
169,47 |
153,61 |
160,16 |
200,97 |
201,86 |
198,03 |
187,74 |
205,69 |
|
6 |
160,11 |
147,75 |
109,29 |
188,97 |
127,93 |
179,33 |
153,42 |
128,49 |
159,80 |
160,55 |
|
7 |
176,62 |
180,02 |
183,43 |
149,66 |
113,64 |
170,37 |
180,74 |
132,75 |
84,58 |
172,97 |
|
8 |
147,27 |
138,01 |
158,67 |
133,01 |
161,65 |
168,27 |
194,75 |
114,29 |
162,36 |
139,61 |
|
9 |
199,99 |
156,53 |
104,26 |
161,36 |
181,23 |
178,00 |
241,30 |
197,14 |
144,12 |
159,39 |
|
10 |
195,72 |
167,66 |
182,20 |
148,29 |
148,13 |
144,22 |
180,65 |
161,10 |
169,07 |
132,26 |
Выполнена аналитическая оценка параметров масштаба, формы и сдвига. Оценки обозначены соответственно — a΄, b΄, c΄ (таблица 3).
Таблица 3
Результаты аналитической оценки параметров
|
Оценки параметров закона Фишера – Типпета |
||
|
a΄ |
b΄ |
c΄ |
|
104,40 |
3,28 |
255,32 |
Закон Фишера – Типпета, в отличие от закона Вейбулла, имеет ограничение справа и задает максимальное значение случайной величины, поэтому для получения вариационного ряда необходимо упорядочить значения набора данных (выборки) от максимума до минимума.
Если объем выборки n ≤ 30, то не рекомендуется группировать данные по интервалам. В данном случае каждой варианте будет присвоен ранг j, а для оценки значений эмпирической функции распределения рекомендовано использовать приближение для медианной позиции рангов [16]:
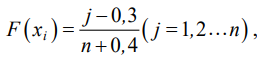 (6)
(6)
где xi — упорядоченное от максимума до минимума значение варианты выборки, соответствующее j-му рангу;
j — порядковый номер ранга; n — объем выборки.
В противном случае при n > 30 необходимо выполнить группировку данных по интервалам в соответствии с абсолютным размахом выборки. При этом количество интервалов k рекомендовано принимать в пределах
7 ≤ k ≤ 40 в зависимости от объема выборки n. Для группировки данных необходимо определить границы интервала, подобрав значения X΄ ≤ xmin и X΄΄ ³ xmax, и разбить полученный интервал [X΄; X΄΄] на интервалы равной длины h:
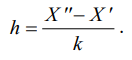 (7)
(7)
Затем следует получить интервальный вариационный ряд, определив количество значений выборки ni, попавших в каждый интервал. Каждый интервал описывается абсциссой Xi, которая определяет позицию распределения упорядоченных данных.
Для средней позиции эмпирическая функция распределения оценивается с помощью выражения:
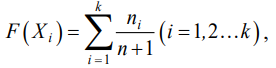 (8)
(8)
где Xi — середина i-го интервала; ni — количество вариант выборки, попавших в i-й интервал; k — количество интервалов; n — объем выборки.
В качестве примера сгруппированы и рассчитаны значения эмпирической функции распределения (рис. 2) для набора данных из таблицы 3.
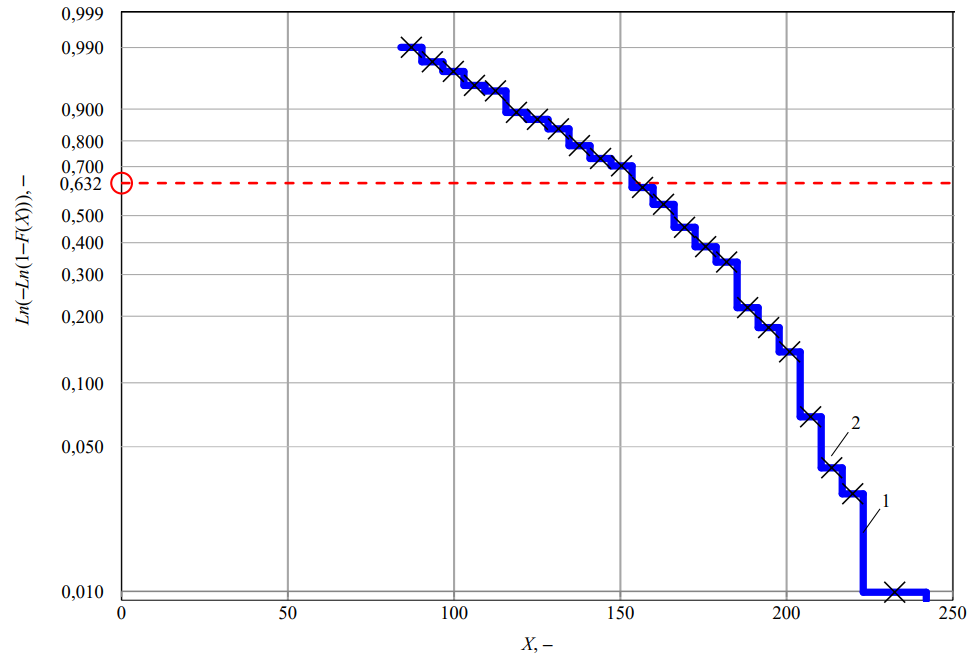
Рис. 2. Эмпирическая функция распределения: 1 — функция; 2 — середина интервала
На рис. 2 по оси ординат указана величина вероятности, по оси абсцисс — значения набора данных (выборки) без определенного физического смысла.
Для группировки данных принято k = 25, X΄ = 84, X΄΄ = 242 и определено значение h = 6,32. Одно значение выборки попало в первые три интервала, поэтому их объединили. Итоговое количество интервалов — k = 23. Результаты вычислений представлены в таблице 4.
Таблица 4
Результаты вычислений
|
i |
Интервал ранга |
ni |
Xi |
F(Хi) |
F(Хi)+F(Хi+1) |
Lg(Xi) |
Ln(–Ln(1–(F(Хi)+F(Хi+1)))) |
C'–Xi |
Lg(C'–Xi) |
|
|
начало |
конец |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1* |
223,04* |
242,00* |
1 |
232,52 |
0,0099 |
0,0099 |
2,3665 |
–4,6101 |
22,68 |
1,3555 |
|
2 |
216,72 |
223,04 |
2 |
219,88 |
0,0198 |
0,0297 |
2,3422 |
–3,5015 |
29,00 |
1,4623 |
|
3 |
210,40 |
216,72 |
1 |
213,56 |
0,0099 |
0,0396 |
2,3295 |
–3,2087 |
35,32 |
1,5480 |
|
4 |
204,08 |
210,40 |
3 |
207,24 |
0,0297 |
0,0693 |
2,3165 |
–2,6335 |
41,64 |
1,6195 |
|
5 |
197,76 |
204,08 |
7 |
200,92 |
0,0693 |
0,1386 |
2,3030 |
–1,9024 |
47,96 |
1,6808 |
|
6 |
191,44 |
197,76 |
4 |
194,60 |
0,0396 |
0,1782 |
2,2891 |
–1,6282 |
54,28 |
1,7346 |
|
7 |
185,12 |
191,44 |
4 |
188,28 |
0,0396 |
0,2178 |
2,2748 |
–1,4038 |
60,60 |
1,7824 |
|
8 |
178,80 |
185,12 |
12 |
181,96 |
0,1188 |
0,3366 |
2,2600 |
–0,8906 |
66,92 |
1,8255 |
|
9 |
172,48 |
178,80 |
5 |
175,64 |
0,0495 |
0,3861 |
2,2446 |
–0,7175 |
73,24 |
1,8647 |
|
10 |
166,16 |
172,48 |
7 |
169,32 |
0,0693 |
0,4554 |
2,2287 |
–0,4979 |
79,56 |
1,9007 |
|
11 |
159,84 |
166,16 |
9 |
163,00 |
0,0891 |
0,5446 |
2,2122 |
–0,2402 |
85,88 |
1,9339 |
|
12 |
153,52 |
159,84 |
7 |
156,68 |
0,0693 |
0,6139 |
2,1950 |
–0,0497 |
92,20 |
1,9647 |
|
13 |
147,20 |
153,52 |
9 |
150,36 |
0,0891 |
0,7030 |
2,1771 |
0,1939 |
98,52 |
1,9935 |
|
14 |
140,88 |
147,20 |
3 |
144,04 |
0,0297 |
0,7327 |
2,1585 |
0,2771 |
104,84 |
2,0205 |
|
15 |
134,56 |
140,88 |
5 |
137,72 |
0,0495 |
0,7822 |
2,1390 |
0,4214 |
111,16 |
2,0459 |
|
16 |
128,24 |
134,56 |
6 |
131,40 |
0,0594 |
0,8416 |
2,1186 |
0,6111 |
117,48 |
2,0699 |
|
17 |
121,92 |
128,24 |
3 |
125,08 |
0,0297 |
0,8713 |
2,0972 |
0,7179 |
123,80 |
2,0927 |
|
18 |
115,60 |
121,92 |
2 |
118,76 |
0,0198 |
0,8911 |
2,0747 |
0,7963 |
130,12 |
2,1143 |
|
19 |
109,28 |
115,60 |
5 |
112,44 |
0,0495 |
0,9406 |
2,0509 |
1,0379 |
136,44 |
2,1349 |
|
20 |
102,96 |
109,28 |
1 |
106,12 |
0,0099 |
0,9505 |
2,0258 |
1,1005 |
142,76 |
2,1546 |
|
21 |
96,64 |
102,96 |
2 |
99,80 |
0,0198 |
0,9703 |
1,9991 |
1,2575 |
149,08 |
2,1734 |
|
22 |
90,32 |
96,64 |
1 |
93,48 |
0,0099 |
0,9802 |
1,9707 |
–4,6101 |
155,40 |
2,1914 |
|
23 |
84,00 |
90,32 |
1 |
87,16 |
0,0099 |
0,9901 |
1,9403 |
–3,5015 |
161,72 |
2,2088 |
где * — корректировка при объединении интервалов 1–3 в один интервал [ 223,04; 242,00].
По оси абсцисс вероятностного графика принимаем шкалу с десятичным логарифмом. Результаты вычислений в столбцах 8 и 9 таблицы 4 определяют координаты точек для построения графика {Lg(Xi); Ln(–Ln(1–(F(Хi)+F(Хi+1))))}.
На следующем этапе оценивается параметр сдвига. Для этого сквозь массив точек (поз. 1 рис. 3) необходимо провести плавную кривую (не прямую) (поз. 2 рис. 3).
В точке пересечения прямой аппроксимирующей точки и прямой с «нулевой» ординатой (поз. 7 рис. 3) выполняется графическая оценка параметра масштаба А΄.
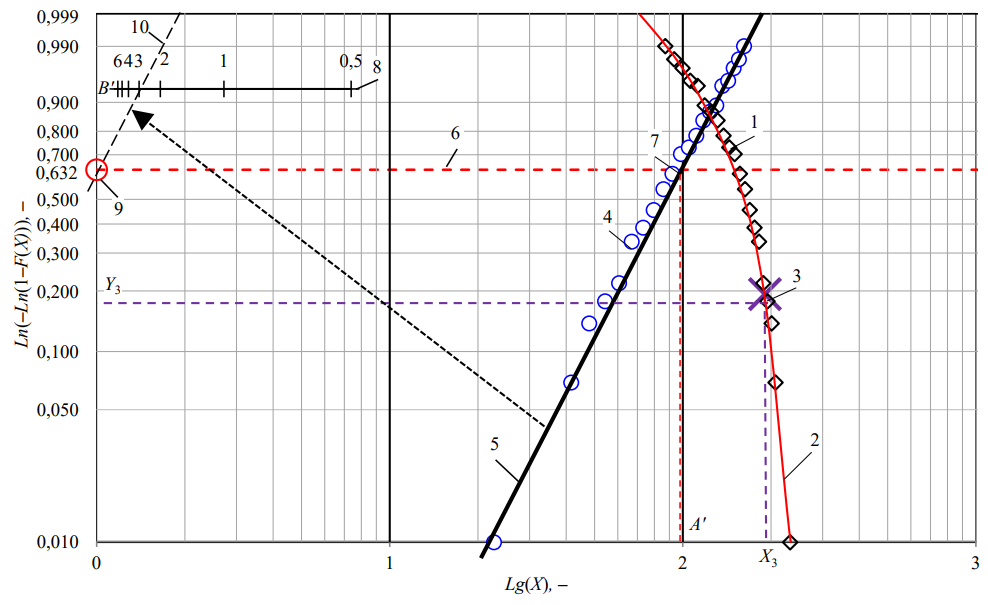
Рис. 3. Графическая оценка параметров закона Фишера – Типпета: 1 — точки с координатами
{Lg(Xi); Ln(–Ln(1–(F(Хi)+F(Хi+1)))}; 2 — линия для оценки абсциссы X3 по ординате Y3; 3 — точка с координатами {Y3; X3};
4 — точки с координатами {Lg(С΄–Xi); Ln(–Ln(1–(F(Хi)+F(Хi+1))))}; 5 — прямая, аппроксимирующая точки 4; 6 — линия для оценки параметра масштаба; 7 — точка пересечения линий 5 и 6, советующая оценке параметра масштаба A΄; 8 — шкала для оценки параметра формы B΄; 9 — точка с координатами {0; 0}; 10 — прямая, проведенная через точку 9 параллельно прямой 5, для оценки параметра формы B΄ по шкале 8
На рис. 3 по оси ординат указана величина вероятности, по оси абсцисс — значения набора данных (выборки) без определенного физического смысла.
Координаты точек крайних членов вариационного ряда обозначаются через {Х1; Y1} и {Х2; Y2}, и оценивается координата Y3:
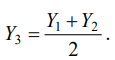 (9)
(9)
С помощью ординаты Y3 на ранее обозначенной кривой следует определить абсциссу Х3 (поз. 3 рис. 3). Затем оценивается параметр сдвига С΄:
 (10)
(10)
В представленном примере крайние члены вариационного ряда — это средние точки интервалов i = 1 и i = 23 с координатами {Lg(X1); Ln(–Ln(1–(F(Х1)))} и {Lg(X23); Ln(–Ln(1–(F(Х22)+F(Х23)))}. Соответственно, Y1 = Ln(–Ln(1–(F(Х1))), Y2 = Ln(–Ln(1–(F(Х22)+F(Х23))), X1 = Lg(X1); X2 = Lg(X23). В результате графическая оценка параметра сдвига С΄ = 248,88. Используем ее для корректировки абсциссы всех точек, определив величины (С΄–Хi), и нанесем на график точки с соответствующими координатами (поз. 4 рис. 3). Как видно, после корректировки точки выстроились «ровнее», что позволяет провести через них прямую линию (поз. 5 рис. 3).
Оценка параметра формы соответствует показателю угла наклона аппроксимирующей прямой (поз. 5 рис. 3) к оси абсцисс. Для графической оценки параметра можно использовать координаты точек или специальную шкалу (при наличии). При оценке параметра формы по координатам необходимо выражать величины по оси абсцисс в масштабе натурального логарифма, т. е. использовать величину Ln(X) вместо Lg(X).
В рассмотренном примере представлена шкала для графической оценки параметра формы B΄ (поз. 8 рис. 3). Для построения шкалы выполнен расчет координат точек {Lg(X); Ln(Y)} по заданным значениям параметра формы (таблица 5). Шкала ориентирована на точку отсчета с координатами {0; 0} (поз. 9 рис. 3). Для оценки параметра формы необходимо через точку отсчета провести прямую, параллельную аппроксимирующей прямой (поз. 10 рис. 3).
Таблица 5
Построение шкалы для графической оценки параметра формы
|
B΄ |
0,5000 |
1,0000 |
2,0000 |
3,0000 |
4,0000 |
5,0000 |
6,0000 |
|
Ln(Y) |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
Ln(X) |
2,0000 |
1,0000 |
0,5000 |
0,3333 |
0,2500 |
0,2000 |
0,1667 |
|
Lg(X) |
0,8686 |
0,4343 |
0,2171 |
0,1448 |
0,1086 |
0,0869 |
0,0724 |
В результате обработки данных получены графические оценки параметров закона Фишера – Типпета (таблица 6).
Таблица 6
Результаты графической оценки параметров
|
Оценки параметров закона Фишера – Типпета |
||
|
A΄ |
B΄ |
С΄ |
|
98,17 |
2,98 |
248,87 |
После оценки параметров необходимо выполнить проверку с помощью обратной функции (5), используя заданные значения вероятностей:
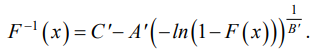 (11)
(11)
Вычислив значения обратной функции распределения (11) и соединив полученные точки на графике, можно визуально оценить качество модели. Как видно, график обратной функции (рис. 4) плавно описывает массив изначальных точек (поз. 1 и 2 рис. 4). Это позволяет сделать вывод, что полученная модель хорошо описывает данные, и оценка параметров выполнена правильно.
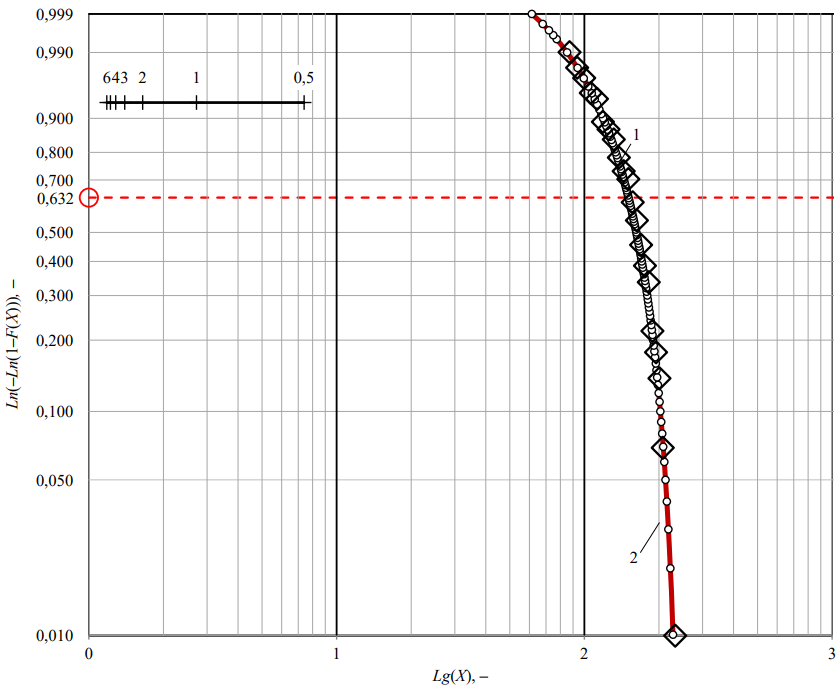
Рис. 4. Проверка модели после графической оценки параметров:
1 — начальные точки с координатами {Lg(Xi); Ln(–Ln(1–(F(Хi)+F(Хi+1)))};
2 — график обратной функции распределения F–1(x) с параметрами A΄, B΄, С΄
На рис. 4 по оси ординат указана величина вероятности, по оси абсцисс — значения набора данных (выборки) без определенного физического смысла.
Результаты поверочных расчетов представлены в таблице 7.
Таблица 7
Результаты проверки полученной модели
|
F(x) |
F–1(x) |
Lg(F–1(x)) |
Ln(–Ln(1–(F(x)) |
|
|
0,0010 |
239,1548 |
2,3787 |
–6,9073 |
|
|
0,0050 |
232,2033 |
2,3576 |
–5,2958 |
|
|
0,0100 |
227,8309 |
2,3068 |
–4,6001 |
|
|
0,0500 |
212,5564 |
2,2775 |
–2,9702 |
|
|
0,1000 |
202,6589 |
2,2537 |
–2,2504 |
|
|
0,2000 |
189,4586 |
2,2317 |
–1,4999 |
|
|
0,3000 |
179,3564 |
2,2096 |
–1,0309 |
|
|
0,4000 |
170,4725 |
2,1862 |
–0,6717 |
|
|
0,5000 |
162,0373 |
2,1596 |
–0,3665 |
|
|
0,6000 |
153,5320 |
2,1263 |
–0,0874 |
|
|
0,7000 |
144,4053 |
2,0758 |
0,1856 |
|
|
0,8000 |
133,7435 |
2,0299 |
0,4759 |
|
|
0,9000 |
119,0766 |
1,9303 |
0,8340 |
|
|
0,9900 |
85,1730 |
1,8882 |
1,5272 |
|
|
0,9990 |
61,3715 |
1,7880 |
1,9326 |
Как видно, графические и аналитические оценки параметров близки к параметрам, заданным при моделировании набора данных (a, b, c).
Сравнивать полученные оценки по отношению к заданным параметрам не совсем корректно, однако такое сравнение оправданно, если принять заданные параметры за истинные параметры генеральной совокупности, а набор случайных данных хi считать репрезентативной выборкой. Сравнительный анализ графических и аналитических оценок представлен в таблице 8.
Таблица 8
Сравнение графических и аналитических оценок параметров
|
Показатель |
Параметр масштаба |
Значение |
δ, % |
Параметр формы |
Значение |
δ, % |
Параметр сдвига |
Значение |
δ, % |
|
Заданные параметры |
a |
100,00 |
– |
b |
3,00 |
– |
c |
250,00 |
– |
|
Аналитическая оценка параметров |
a΄ |
104,40 |
4,40 |
b΄ |
3,28 |
9,33 |
c΄ |
255,32 |
2,13 |
|
Графическая оценка параметров |
A΄ |
98,17 |
1,83 |
B΄ |
2,98 |
0,67 |
С΄ |
248,87 |
0,45 |
Сравнительный анализ показал, что относительная погрешность графических оценок не превышает 2 % (δ < 2 %). Погрешность аналитических оценок в данном примере оказалась выше, но это не значит, что аналитический метод менее точен.
Обсуждение и заключение. Представленный метод вероятностной сетки для закона Фишера – Типпета адекватен и подходит для практического применения. Например, его можно использовать в программных комплексах или при создании пользовательских приложений для графического представления результатов статистического анализа. Открывается возможность выполнять подгонку модели совместно с другими известными методами, в том числе если они несостоятельны. Предложенную методику построения шкалы для графической оценки параметра формы можно применять при оценке параметра формы закона Вейбулла. Полученные аналитические зависимости, положения методики и графический материал могут быть полезны при разработке соответствующего национального стандарта.
1. ГОСТ Р ИСО 16269–4–2017. Статистические методы. Статистическое представление данных. Часть 4. Выявление и обработка выбросов. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200146680 (дата обращения: 15.01.2025).
2. ГОСТ Р 50779.27–2017. Статистические методы. Распределение Вейбулла. Анализ данных. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200146523 (дата обращения: 15.01.2025).
3. ГОСТ ISO 7870–1–2022. Статистические методы. Контрольные карты. Часть 1. Общие принципы. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200192703 (дата обращения: 15.01.2025).
4. ГОСТ 11.008–75. Прикладная статистика. Графические методы обработки данных. Метод вероятностных сеток. URL: https://meganorm.ru/Data2/1/4294753/4294753131.pdf (дата обращения: 15.01.2025).
Список литературы
1. Дерябин М.А., Бавыкин О.Б., Дьяков Д.А. Применение метода вероятностной бумаги для определения закона распределения результатов измерений. В: Труды II Международной научно-практической конференции «Современные тенденции развития науки и образования: Теория и практика». Москва: Институт системных технологий; 2018. С. 67–72.
2. Добротин С.А., Косырева О.Н. Оценка наличия выбросов в данных времени удерживания при хроматографическом анализе. В: Труды Международной научно-практической конференции Science and technology research — 2024. Петрозаводск: Новая наука; 2024 С. 11–22. URL: https://sciencen.org/assets/Kontent/Konferencii/Arhiv-konferencij/KOF-971.pdf?ysclid=m6huh354xe556269601 (дата обращения: 15.01.2025).
3. Шпер В.Л. Инструменты качества и не только! Часть 5. Анализ закона распределения с помощью вероятностных сеток. Методы менеджмента качества. 2021;8:54–60.
4. Буланов Я.И., Мошкало Н.Г., Курденкова А.В., Шустов Ю.С., Малюга Д.К. Установление эмпирических законов распределения для определяющих показателей качества параарамидных тканей для бронепакетов с антипрорезными и антипрокольными свойствами. Известия высших учебных заведений. Технология легкой промышленности. 2023;59(1):106–109. https://doi.org/10.46418/0021-3489_2023_59_01_20
5. Аблазова К.С. Контрольные карты, определяющие стабильность технологического процесса, и их приложения. Проблемы вычислительной и прикладной математики. 2023;3(49):124–134.
6. Великанова Н.П., Великанов П.Г. Изменение жаропрочности материала рабочих лопаток турбины с учетом влияния эксплуатационной наработки. Экологический вестник научных центров Черноморского экономического сотрудничества. 2023;20(2):42–48. https://doi.org/10.31429/vestnik-20-2-42-48
7. Хазанович Г.Ш., Апрышкин Д.С. Оценка влияния внутренних факторов на показатели загруженности пассажирских лифтовых установок на основе результатов регулярного мониторинга. Безопасность техногенных и природных систем. 2023;7(3):34–43. https://doi.org/10.23947/2541-9129-2023-7-3-34-43
8. Касьянов В.Е., Демченко Д.Б., Косенко Е.Е., Теплякова С.В. Метод оптимизации надежности машин с применением интегрального показателя. Безопасность техногенных и природных систем. 2020;1:23–31. https://doi.org/10.23947/2541-9129-2020-1-23-31
9. Котесов А.А. Усеченная форма закона Фишера – Типпета для моделирования нагруженности машиностроительных конструкций. Безопасность техногенных и природных систем. 2024;8(4):39–46. https://doi.org/10.23947/2541-9129-2024-8-4-39-46
10. Fisher RA, Tippet LHC. Limiting Forms of the Frequency Distribution of the Longest of Smallest Member of Sample. Mathematical Proceedings of the Cambridge Philosophical Society. 1928;24(2),180–190. https://doi.org/10.1017/S0305004100015681
11. Котесов А.А., Котесова А.А. Комплексная корректировка параметров выборочных распределений характеристик прочности и нагруженности при оптимизации показателей надежности объектов машиностроения. Известия Тульского государственного университета. Технические науки. 2023;8:699–708. https://doi.org/10.24412/2071-6168-2023-8-699-700
12. Lawless JF. Statistical Models and Methods for Lifetime Data, 2nd ed. Hoboken: Wiley; 2011. 664 p.
13. Ross R. Graphical Methods for Plotting and Evaluating Weibull Distributed Data. In: Proc. of 1994 4th International Conference on Properties and Applications of Dielectric Materials (ICPADM). Brisbane, QLD, Australia; 1994. P. 250–253 http://doi.org/10.1109/ICPADM.1994.413986
14. Hyndman RJ, Yanan Fan. Sample Quantiles in Statistical Packages. The American Statistician. 1996;50(4):361–365. http://doi.org/10.1080/00031305.1996.10473566
15. Makkonen L, Pajari M, Tikanmäki M. Discussion on “Plotting Positions for Fitting Distributions and Extreme Value Analysis”. Canadian Journal of Civil Engineering. 2013;40(9):927–929. https://doi.org/10.1139/cjce-2013-0227
16. Benard A, Bos-Levenbach EC. Het uitzetten van waarnemingen op waarschijnlijkheids-papier. Statistica Neerlandica. 1953;7(3):163–173. https://www.sci-hub.ru/10.1111/j.14679574.1953.tb00821.x?ysclid=m6hw1ukl7k731787987
Об авторе
А. А. КотесовРоссия
Анатолий Анатольевич Котесов, кандидат технических наук, доцент кафедры эксплуатации транспортных систем и логистики
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Котесов А.А. Метод вероятностной сетки для закона Фишера – Типпета. Безопасность техногенных и природных систем. 2025;(2):146-157. https://doi.org/10.23947/2541-9129-2025-9-2-146-157. EDN: TCVEAL
For citation:
Kotesov A.A. Probability Grid Method for Fisher-Tippett Law. Safety of Technogenic and Natural Systems. 2025;(2):146-157. https://doi.org/10.23947/2541-9129-2025-9-2-146-157. EDN: TCVEAL








































