Modeling the Dynamics of Harmful Phytoplankton Species Concentration in Taganrog Bay of the Azov Sea

Introduction. The excessive growth of harmful phytoplankton is a problem in many water bodies in Russia and around the world. Coastal estuarine systems, such as Taganrog Bay, are particularly vulnerable to this issue due to several factors: high nutrient runoff from rivers, consistent warming due to shallow depths, and differences in depth and salinity. These outbreaks of potentially toxic algae blooms pose a threat to local communities, harm fish populations, and can lead to oxygen depletion and other negative consequences. In Taganrog Bay, microalgae belonging to the cyanophyte are particularly dangerous. Their biomass can reach up to 70% in the summer, and in some cases, it can even reach 90% of total phytoplankton [1].

Cyanophytes are also called cyanobacteria, or less formally blue-green algae. This type of phytoplankton is distinguished from other species by several features that are advantages in their competition for resources, which explains the high proportion of their biomass. First of all, cyanobacteria are prokaryotes and have a very simple cell structure similar to a bacterial one, without a nucleus, mitochondria, Golgi apparatus or endoplasmic reticulum. Individually, cyanophytes are small compared to other algae species, but they often form massive colonies or filaments. The buoyancy of blue-green algae is provided by gas vacuoles, which allow them to change their density, which leads to their movement in the water column in a vertical direction [2]. This mechanism provides better access to either light or nutrients [3], and the presence of nutrients in the reservoir plays a major role in changing its density [4]. All this gives cyanobacteria an advantage over other types of plankton. In addition, turbulent diffusion and the velocity of movement of the aquatic environment in the vertical direction can affect the vertical migration of cyanobacteria [5].

In coastal ecosystems, cyanobacteria have been of interest due to their potential toxicity and their role in the production of phytoplankton. These bacteria release toxins that vary in nature depending on the species, and can be neurotoxic, hepatotoxic, or endotoxic. However, not all blooms of cyanobacteria release toxins. Currently, researchers are studying the nature of these toxins and the conditions that cause their release [6].

Aphanizomenon flos-aquae, Microcystis aeruginosa, and Anabaena spp. are the most common species found in the waters of Taganrog Bay. These species can produce toxins related to hepatotoxins and neurotoxins [7].

Many domestic and foreign researchers have devoted their works to the study of potentially harmful cyanobacterial blooms. In [8], the role of phosphorus in promoting the growth of blue-green algae was investigated. In study [9], the process of vertical movement of cyanobacteria of the Microcystis species was modeled, which allows them to dominate during the bloom period in reservoirs. The effect of the intensity of light radiation and mixing of waters under the action of wind on the development of algae was modeled using the Ansys Fluent and MATLAB systems, which is described in [10]. The authors of research [11] used autoregressive and multidimensional versions of linear regression, random forest, and Long Short-Term Memory (LSTM) neural networks to predict the development of blue-green algae. In [12], a nonstationary three-component mathematical model was proposed to study the competition between two types of phytoplankton (including toxic ones) and their absorption by zooplankton.

The review of modern research conducted by the authors revealed a gap in scientific knowledge, which consists in the lack of an integrated approach linking the authors' model of phytoplankton population dynamics based on convection-diffusion equations with the hydrodynamic model, ignoring the influence of abiotic factors, using one-, two-dimensional models and ready-made software packages that do not provide reliable results for coastal systems. The authors believe that this issue can be addressed by applying an integrated approach to modeling phytoplankton dynamics in the coastal systems of Taganrog Bay. This approach would take into account their important features: significant differences in depth, salinity, complex geometry of the calculated area, increased influx of nutrients, etc.

According to Decree of the Government of the Russian Federation No. 219 dated April 10, 2007, one of the goals of monitoring water bodies is “timely identification and forecasting of the negative effects to water, as well as the development of negative processes affecting water quality in water bodies and their condition, the development and implementation of measures to prevent the negative effects of these processes”¹. The development of mathematical modeling methods and the development of software systems based on them make it possible to obtain forecasts of the development of dangerous phenomena in complex natural systems. Such data can be shared with decision makers to monitor and manage the situation in coastal areas. One of the ways to restore Taganrog Bay may be to replace blue-green algae with green ones. It is noted in [13] that in those areas of the reservoir where the number of green algae has increased in relation to blue-green and diatoms, the ability of the water body to self-purify has increased. In [14], the dynamics of microalgae development in drinking water intake sites was studied, the depressing effect of cyanobacteria blooming was noted, and a system for monitoring the dynamics of phytoplankton populations was proposed.

Due to the need to predict the occurrence of harmful “blooms” of microalgae, it is necessary to construct complex mathematical models of phytoplankton population development. These models should take into account advective and diffusive transfers, weather conditions, and geometry of the calculated area, limiting the growth of microalgae by the presence of nutrients, salinity and temperature regimes [15]. The use of mathematical methods proposed in this article is justified because they provide a high level of accuracy in modeling processes occurring in complex natural systems, using a small amount of input data. Additionally, these methods are more cost-effective than conducting expeditionary research.

The aim of this research is to make a medium-term prediction of the development of blue-green algae during the bloom season using mathematical modeling methods. To achieve this, the authors have solved the following tasks:

1. Construction of a mathematical model of phytoplankton populations, supplemented by initial and boundary conditions. The model was equipped with input data: values of the vector of the water flow obtained on the basis of the model of hydrodynamics, indicators of depths, salinity and temperature, concentrations of blue-green and green algae, as well as compounds of biogenic substances based on the results of long-term observations.
2. The values of water depth, salinity, and temperature were distributed according to cartographic information using the authors' interpolation algorithm.
3. A difference analogue of the continual problem was constructed.
4. A model of the dynamics of phytoplankton populations was implemented in the form of a software module.

Materials and Methods. The study was based on a three-dimensional model of the dynamics of phytoplankton populations based on a system of convection-diffusion-reaction equations with nonlinear source functions. The difference approximation of the model was based on explicit-implicit splitting schemes. The authors' method of interpolation of depth values was used to construct a three-dimensional computational domain. It was also used to interpolate salinity and temperature values from cartographic information.

A three-dimensional model of the dynamics of phytoplankton populations was developed based on the work of Sukhinov A.I. and Yakusheva E.V. [16][17]. The model was based on a system of non-steady convection-diffusion-reaction equations:

(1)

where q_i — concentration of the i-th component, mg/l, 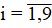; V = (u, v, w) — vector of the water flow velocity, m/s; μ = {μ, μ, v} — turbulent exchange coefficients, m²/s;  — nonlinear function-source of nutrients, mg/(l s); ∇ — gradient; 1 —Aphanizomenon flos-aquae blue-green algae (potentially toxic; 2 —Chlorella Vulgaris green algae (included in the base of the food pyramid); 3 — dissolved organic phosphorus; 4 — suspended organic phosphorus; 5 — phosphates; 6 — nitrates; 7 — nitrites; 8 — ammonia; 9 — dissolved oxygen: it mainly enters the aquatic environment from the surface of a reservoir as a result of mixing (mainly waves caused by wind), is released by aquatic plants during photosynthesis in the presence of light and is consumed during respiration in the absence of light.

The equations describing the transformation cycles of the simulated substances are given in [18].

The growth rate of phytoplankton populations was determined by the availability of nutrients (phosphates, nitrates, nitrites and ammonium), optimal values of temperature, salinity and illumination. Biomass decreased due to excretion and death. Green algae compete with cyanobacteria for resources. The growth rate of phytoplankton populations was expressed as a function of salinity S, temperature T, light intensity I, and a sufficient number of dissolved oxygen molecules in the water. Also, the growth of microalgae depended on the concentration of the main nutrients — nitrogen compounds (nitrates NO₃, nitrites NO₂, ammonia NH₄) and phosphorus (phosphates, dissolved organic phosphorus DOR, suspended organic phosphorus ROP). An initial boundary value problem was set for system (1), and the corresponding initial and boundary conditions were added [18].

The numerical solution to the problem of phytoplankton population dynamics was to transform the input data using mathematical modeling methods. When solving problem (1), the values of the components of the vector of the water flow in the nodes of the computational grid were used as input data. It was calculated based on the model of hydrodynamics [19], values of salinity S₀, temperature T₀ and concentrations q_0i at time t₀. For the difference approximation, the modeling area was covered by a computational grid μω ω_τ × ω_h that was uniform in time and three spatial directions:

,

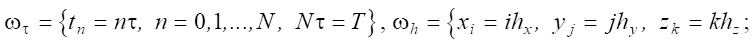
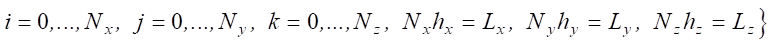where τ — step in time, 0 ≤ t ≤ T; h_x, h_y, h_z — steps in spatial directions; L_x, L_y, L_z — maximum size of the calculated area in space.

Explicit and implicit schemes were used to discretize problem (1):

,

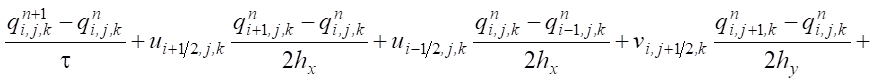
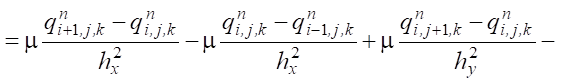
where q^n+σ = σ qⁿ⁺¹ + (1 – σ)qⁿ, σ ∈ [0,1] — weight of the scheme.

The result of applying this approach to the approximation of the convection-diffusion-reaction equations led to a series of two-dimensional and one-dimensional problems. Along the Ox and Oy axes, the approximation was done using a symmetric scheme with weights (Crank-Nicolson). Along the Oz axis, an explicit scheme was used, and a run-through method was used for software implementation

The authors' method of interpolating the values of depth, salinity, and temperature was used to construct a uniform space-time grid. Cartographic information was used to define the boundaries of the computing area vertically, for example, pilot charts used for the needs of the shipping and fishing industries. Often, information about the depths of a reservoir was set at certain points or by level isolines and may not be present at the points of the calculated grid. Figure 1 shows the initial relief image of the bottom of the Azov Sea, where the depths were indicated by level isolines.

Such maps did not have a high degree of smoothness at the points of joining, so the interpolation algorithm was used in this study [20]. In order to construct a function of the bottom topography with a high degree of smoothness, an equation was solved:

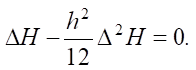(2)

The fundamental system of solutions of equation (2) had the form:

(3)

The depth values were interpolated based on the splines of function (3).

The algorithm of the program module was as follows: a file in the .txt format was submitted as input, containing an array with depth isolines or points indicating the depths. Then a fourth-order accuracy scheme was constructed for the diffusion transfer operator [20]. The resulting grid equations were solved using an adaptive, modified alternating triangular variational method. The output was a text file containing an array of values of the depths of the Azov Sea.

Results. As a result of the research, the authors obtained a medium-term forecast of the distribution of blue-green and green algae based on an integrated approach using models of phytoplankton population dynamics and hydrodynamics. Figure 2 shows the result of the authors' algorithm, a reconstructed map of the depths of the Azov Sea.

Based on the developed method, sufficiently smooth distributions of salinity and temperature values suitable for modeling were also obtained, the images of which are shown in Figure 3.

The obtained distributions of depths, salinity, and temperature were used as input data for solving problem (1). Figure 4 shows the concentrations of two phytoplankton populations obtained as a result of the computational experiment. Uniform distributions of the simulated substances were input data for the software module, with a time interval of 30 days.

Discussion. The interpolations of the distributions of depths, salinity, and temperature, obtained using the algorithm presented in this paper, have a sufficient degree of smoothness at the points where they are joined. A computational experiment has shown that the range of blue-green algae is wider than that of green algae — they are distributed throughout Taganrog Bay and carried by currents into the main part of the Azov Sea.

The mathematical model of phytoplankton population dynamics takes into account several factors, including the limitation of microalgae growth by nutrients, the influence of the hydrological regime on the growth coefficient, geographical dynamics under the influence of convection and diffusion processes, and the oxygen regime. By combining this model with a hydrodynamic model, it is possible to create three-dimensional images of the distribution of substances being modeled. This allows for the consideration of not only the biological aspects of phytoplankton growth but also the spatio-temporal dynamics of biomass and the shape of the computational area.

Conclusion. The described mathematical model and the proposed methods have been integrated into the Azov3D software package. This allows us to predict the development of hazardous blooms of phytoplankton (eutrophication) under different weather conditions, taking into account changes in salinity, temperature, current patterns, nutrient availability, and oxygen regime. The forecasts generated can be used to develop a strategy for the sustainable management of Taganrog Bay, an important natural area. Various strategies for managing this aquatic ecosystem are currently being developed, as well as safety mechanisms to prevent suffocation and eutrophication events. Mathematical modeling techniques, the development of which is discussed in this article, provide inexpensive and efficient tools for monitoring and predicting the state of aquatic systems.