Перейти к:
Моделирование динамики концентрации вредоносных видов фитопланктона в Таганрогском заливе Азовского моря
https://doi.org/10.23947/2541-9129-2025-9-4-284-293
EDN: YTBWWQ
Аннотация
Введение. Исследователи из Южного научного центра РАН путем натурных измерений неоднократно фиксировали обильные «цветения» микроводорослей в Таганрогском заливе. В связи с уменьшением биоразнообразия и ухудшением качества вод Азовского моря вследствие сокращения пресноводного стока, повышения температуры воды и увеличенного притока биогенных веществ риск развития токсичных фитопланктонных популяций еще больше возрастает, что непосредственно угрожает всей экосистеме, экономике региона и здоровью местного населения. Повышение среднегодовой температуры, увеличение объема поступлений соединений азота и фосфора как последствий урбанизации и деятельности сельскохозяйственных предприятий приводят к ускоренному росту цианобактерий, которое сопровождается обильным цветением и потенциальной токсичностью, особенно в Таганрогском заливе. В настоящее время, чтобы отслеживать изменения концентрации фитопланктонных популяций, используются модели на уровне лаг-процедур и реактивных норм. Однако применение их в условиях Азовского моря требует учета специфики перепадов глубин, солености и сезонных характеристик, то есть комплексного подхода к определению концентрации вредного планктона. В связи с этим целью данного исследования является построение среднесрочных прогнозов развития цианобактерий с использованием комплексного подхода к определению концентрации планктона, основанного на применении методов математического моделирования.
Материалы и методы. Прогнозирование динамики фитопланктонных популяций осуществлялось на основе трехмерной нестационарной математической модели, основанной на системе нестационарных уравнений в частных производных с нелинейными функциями источников. Входными данными для модели являлись значения компонент вектора водного потока, полученные на основе модели гидродинамики, а показатели солености, температуры, концентрации биогенных веществ и фитопланктонных популяций взяты из результатов многолетних наблюдений. Разностная аппроксимация модели выполнена на основе явно-неявных схем расщепления. Для построения трехмерной области вычислений использовался метод интерполяции значений глубин. Также этот метод применен для интерполяции значений солености и температуры по картографической информации.
Результаты исследования. В ходе численного эксперимента, проведенного с учетом влияния солености и температуры, лимитирования биогенными веществами фитопланктонных популяций получены трехмерные изображения распределения цианобактерий и зеленых водорослей в Таганрогском заливе в вегетационный период. Результатом применения метода интерполяции стали достаточно гладкие в точках склейки карты глубин, распределения солености и температуры, которые являются входными данными для разработанной модели по определению динамики концентрации вредоносных видов фитопланктона.
Обсуждение. Представленная в работе математическая модель динамики фитопланктонных популяций учитывает условия развития синезеленых и зеленых водорослей, оказываемое на них влияние со стороны окружающей среды. Она позволяет получать трехмерное изображение распределения планктона и дает возможность определять ареал распространения синезеленых и зеленых водорослей в Таганрогском заливе и в Азовском море.
Заключение. Описанные математическая модель и методы математического моделирования встроены в программный комплекс, что дает возможность моделировать и прогнозировать все изменения, которые происходят и будут происходить в водах Таганрогского залива. Это, несомненно, будет способствовать принятию обоснованных решений в деле дальнейшего развития акватории Азовского моря.
Ключевые слова
Для цитирования:
Белова Ю.В., Чистяков А.Е. Моделирование динамики концентрации вредоносных видов фитопланктона в Таганрогском заливе Азовского моря. Безопасность техногенных и природных систем. 2025;9(4):284-293. https://doi.org/10.23947/2541-9129-2025-9-4-284-293. EDN: YTBWWQ
For citation:
Belova Yu.V., Chistyakov A.E. Modeling the Dynamics of Harmful Phytoplankton Species Concentration in Taganrog Bay of the Azov Sea. Safety of Technogenic and Natural Systems. 2025;9(4):284-293. https://doi.org/10.23947/2541-9129-2025-9-4-284-293. EDN: YTBWWQ
Введение. Обильное цветение вредоносных видов фитопланктона является проблемой многих водоемов России и всего мира. В большей мере этому процессу подвержены прибрежные системы эстуарного типа, такие как Таганрогский залив, в силу ряда особенностей: обильный сток биогенных веществ с речными водами, равномерный прогрев из-за небольшой глубины, перепады глубин и солености. Вспышки цветения потенциально токсичных водорослей несут угрозу здоровью местного населения, наносят вред рыбному хозяйству, могут приводить к заморным явлениям и другим негативным последствиям. В Таганрогском заливе опасными являются микроводоросли, относящиеся к отделу цианофит, их биомасса в летний период составляет около 70 %, а иногда достигает 90 % от общей биомассы фитопланктона [1].
Цианофиты также называют цианобактериями, или менее формально синезелеными водорослями. Этот вид фитопланктона отличают от других видов несколько особенностей, являющихся преимуществами в их конкурентной борьбе за ресурсы, что и объясняет высокую долю их биомассы. В первую очередь, цианобактерии являются прокариотами и имеют очень простую клеточную структуру, подобную бактериальной, без ядра, митохондрий, аппарата Гольджи или эндоплазматической сети. По отдельности цианофиты невелики, по сравнению с другими видами водорослей, но они часто образуют массивные колонии или нити. Плавучесть синезеленым водорослям обеспечивают газовые вакуоли, которые позволяют им менять плотность, что приводит к движению их в водной толще в вертикальном направлении [2]. Такой механизм обеспечивает лучший доступ либо к свету, либо к питательным веществам [3], а наличие питательных веществ в водоеме играет большую роль в изменении плотности [4]. Все это дает цианобактериям преимущество перед другими видами планктона. Кроме того, турбулентная диффузия и скорость движения водной среды в вертикальном направлении могут влиять на вертикальную миграцию цианобактерий [5].
В прибрежных системах цианобактерии представляют интерес по причине их потенциальной токсичности, они к тому же играют важную роль в производстве первичной продукции фитопланктона. Токсины, выделяемые цианобактериями, у разных видов свои и могут быть нейротоксинами, гепатотоксинами или эндотоксинами. Токсины не всегда выделяются во время цветения. В настоящее время проводятся исследования, направленные на изучение природы токсинов и факторов, вызывающих их выделение [6].
В водах Таганрогского залива наиболее распространены Aphanizomenon flos-aquae, Microcystis aeruginosa, Anabaena spp. Эти виды могут выделять яды, относящиеся к гепатотоксинам и нейротоксинам [7].
Исследованию цветения потенциально вредоносных цианобактерий посвящено множество отечественных и зарубежных работ. В работе [8] исследуется роль фосфора в стимулировании развития синезеленых водорослей. В исследовании [9] моделируется процесс вертикального движения цианобактерий вида Microcystis, которое позволяет им занимать доминирующее положение в период цветения водоема. Влияние интенсивности светового излучения и перемешивания вод под действием ветра на развитие водорослей моделировалось с помощью систем Ansys Fluent и MATLAB, что описано в работе [10]. Авторами исследования [11] для прогнозирования развития синезеленых водорослей использовались авторегрессионные и многомерные версии линейной регрессии, случайного леса и нейронных сетей Long Short-Term Memory (LSTM). В работе [12] предлагается нестационарная трехкомпонентная математическая модель для изучения конкуренции между двумя типами фитопланктона (в том числе токсичного) и поглощения их зоопланктоном.
Проведенный авторами обзор современных исследований выявил пробел в научном знании, который заключается в отсутствии комплексного подхода, связывающего авторскую модель динамики фитопланктонных популяций, построенную на основе уравнений конвекции-диффузии, с моделью гидродинамики, в игнорировании влияния абиотических факторов, в использовании одно-, двумерных моделей и готовых комплексов программ, не дающих достоверных результатов для прибрежных систем. Авторы исследования считают, что этот пробел возможно устранить путем применения комплексного подхода к моделированию динамики фитопланктона в прибрежных системах Таганрогского залива, который учитывал бы их существенные особенности: значительные перепады глубин, солености, сложную геометрию расчетной области, повышенный приток биогенных веществ и др.
Согласно постановлению Правительства РФ № 219 от 10 апреля 2007 г., одной из целей мониторинга водных объектов является «своевременное выявление и прогнозирование негативного воздействия вод, а также развития негативных процессов, влияющих на качество воды в водных объектах и их состояние, разработка и реализация мер по предотвращению негативных последствий этих процессов»1. Развитие методов математического моделирования и разработка на их основе программных комплексов позволяют получать прогнозы развития опасных явлений в сложных природных системах. Такие данные могут быть переданы лицам, принимающим решения, для контроля и управления ситуацией в прибрежных районах. Одним из способов реабилитации Таганрогского залива могут стать меры по замещению синезеленых водорослей зелеными. В работе [13] отмечается, что в тех областях водоема, где увеличилось количество зеленых водорослей по отношению к синезеленым и диатомовым, повысилась способность водного объекта к самоочищению. В работе [14] исследована динамика развития микроводорослей в местах забора питьевой воды, отмечено угнетающее влияние цветения цианобактерий, предложена система мониторинга динамики фитопланктонных популяций.
В связи с необходимостью прогнозировать возникновение опасных «цветений» микроводорослей построение комплексных математических моделей развития фитопланктонных популяций (с учетом адвективного и диффузионного переносов, погодных условий, геометрии расчетной области, лимитирования роста микроводорослей наличием питательных веществ, режимов солености и температуры [15]) обладает высокой актуальностью. Применение предложенных в статье математических методов обусловлено тем, что они дают достаточно высокую точность моделирования процессов, происходящих в сложных природных системах при небольшом наборе входных данных, а также выходят дешевле, чем экспедиционные исследования.
Целью данного исследования является среднесрочное прогнозирование развития синезеленых водорослей в период вегетации с применением методов математического моделирования. Для этого авторами решены следующие задачи:
- Построение математической модели фитопланктонных популяций, дополненной начальными и граничными условиями. Модель оснащена входными данными: значениями вектора водного потока, полученными на основе модели гидродинамики, показателями глубин, солености и температуры, концентраций синезеленых и зеленых водорослей, а также соединений биогенных веществ, основанных на результатах многолетних наблюдений.
- По картографической информации с применением авторского алгоритма интерполяции распределены значения глубин, солености и температуры воды.
- Построен разностный аналог непрерывной задачи.
- Реализована модель динамики фитопланктонных популяций в виде программного модуля.
Материалы и методы. Исследование основывается на трехмерной модели динамики фитопланктонных популяций, построенной на системе уравнений конвекции-диффузии-реакции с нелинейными функциями источников. Разностная аппроксимация модели выполнена на основе явно-неявных схем расщепления. Для построения трехмерной области вычислений применен авторский метод интерполяции значений глубин. Он также использован для интерполяции значений солености и температуры по картографической информации
Трехмерная модель динамики фитопланктонных популяций базируется на работах Сухинова А.И., Якушева Е.В. [16][17] и строится на системе нестационарных уравнений конвекции-диффузии-реакции:
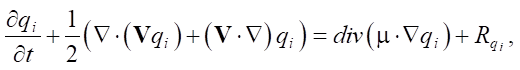 (1)
(1)
где qi — концентрация i-ой компоненты, мг/л, 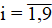 ; V = (u, v, w) — вектор скорости водного потока, м/с; μ = {μ, μ, v} — коэффициенты турбулентного обмена, м²/с;
; V = (u, v, w) — вектор скорости водного потока, м/с; μ = {μ, μ, v} — коэффициенты турбулентного обмена, м²/с; 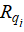 — нелинейная функция-источник биогенных веществ, мг/(л с); ∇ — градиент; 1 — синезеленая водоросль Aphanizomenon flos-aquae (потенциально токсичная; 2 — зеленая водоросль Chlorella Vulgaris (входит в основание пищевой пирамиды); 3 — растворенный органический фосфор; 4 — взвешенный органический фосфор; 5 — фосфаты; 6 — нитраты; 7 — нитриты; 8 — аммиак; 9 — растворенный кислород: в основном попадает в водную среду с поверхности водоема в результате перемешивания (главным образом волнения под действием ветра), выделяется водными растениями в процессе фотосинтеза при наличии света и потребляется в процессе дыхания при отсутствии света.
— нелинейная функция-источник биогенных веществ, мг/(л с); ∇ — градиент; 1 — синезеленая водоросль Aphanizomenon flos-aquae (потенциально токсичная; 2 — зеленая водоросль Chlorella Vulgaris (входит в основание пищевой пирамиды); 3 — растворенный органический фосфор; 4 — взвешенный органический фосфор; 5 — фосфаты; 6 — нитраты; 7 — нитриты; 8 — аммиак; 9 — растворенный кислород: в основном попадает в водную среду с поверхности водоема в результате перемешивания (главным образом волнения под действием ветра), выделяется водными растениями в процессе фотосинтеза при наличии света и потребляется в процессе дыхания при отсутствии света.
Уравнения, описывающие циклы превращений моделируемых субстанций, приведены в работе [18].
Скорость роста фитопланктонных популяций определяется наличием питательных веществ (фосфатов, нитратов, нитритов и аммония), оптимальностью значений температуры, солености и освещенности. Биомасса уменьшается за счет экскреции и отмирания. Зеленые водоросли конкурируют с цианобактериями за ресурсы. Скорость роста фитопланктонных популяций выражается функцией зависимости от солености S, температуры T, освещенности I и достаточного количества молекул растворенного кислорода в воде. Также рост микроводорослей зависит от концентрации основных питательных веществ — соединений азота (нитраты NO3, нитриты NO2, аммиак NH4) и фосфора (фосфаты PO4, растворенный органический фосфор DОР, взвешенный органический фосфор РОР). Для системы (1) ставится начально-краевая задача, добавляются соответствующие начальные и граничные условия [18].
Численное решение задачи динамики фитопланктонных популяций заключается в преобразовании входных данных с использованием методов математического моделирования. При решении задачи (1) в качестве входных данных используются значения компонент вектора водного потока в узлах расчетной сетки, он рассчитывается на основе модели гидродинамики [19], значений солености 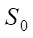 , температуры
, температуры 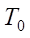 и концентраций q0i в момент времени t0.
и концентраций q0i в момент времени t0.
Для разностной аппроксимации область моделирования покрывается расчетной сеткой 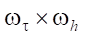 , равномерной по времени и трем пространственным направлениям:
, равномерной по времени и трем пространственным направлениям:
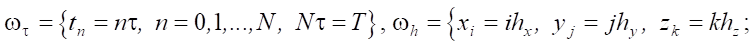
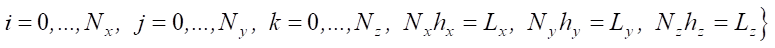 ,
,
где τ — шаг по времени, 0 ≤ t ≤ T; hx, hy, hz — шаги в пространственных направлениях; Lx, Ly, Lz — максимальные размеры расчетной области в пространстве.
Для дискретизация задачи (1) использованы явно-неявные схемы:
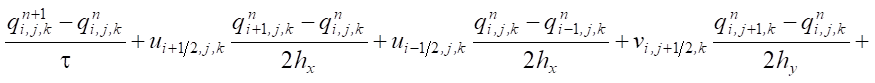
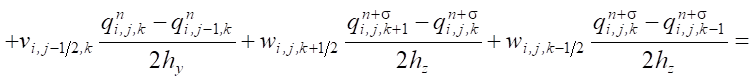
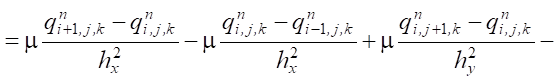
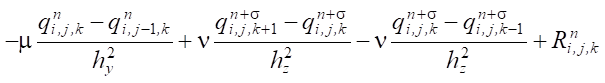 ,
,
где qn+σ = σ qn+1 + (1 – σ)qn, σ ∈ [0,1] — вес схемы.
Результатом применения такого подхода к аппроксимации уравнений конвекции-диффузии-реакции является цепочка двумерно-одномерных задач. В направлении осей Ox и Oy аппроксимация производится симметричной схемой с весами (Кранка-Николсона). В направлении оси Oz используется явная схема, а для программной реализации — метод прогонки.
Авторский метод интерполяции значений глубин, солености и температуры применен для построения равномерной пространственно-временной сетки. Для определения границ области вычислений по вертикали используется картографическая информация, например лоцманские карты, применяемые для нужд судоходства и рыболовной промышленности. Часто информация о глубинах водоема задана в определенных точках или изолиниями уровня и может отсутствовать в точках расчетной сетки. На рис. 1 приведено исходное изображение рельефа дна Азовского моря, на котором глубины обозначены изолиниями уровня.
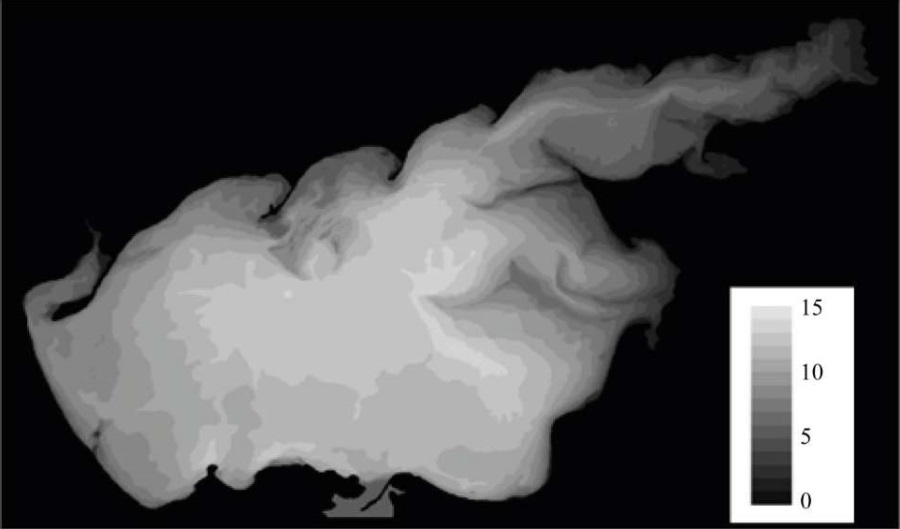
Рис. 1. Изолинии уровня глубин Азовского моря
Подобные карты не обладают достаточной степенью гладкости в точках склейки, поэтому в данной работе применен алгоритм интерполяции [20]. Для построения функции рельефа дна с достаточной степенью гладкости решается уравнение:
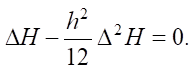 (2)
(2)
Фундаментальная система решений уравнения (2) имеет вид:
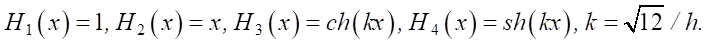 (3)
(3)
Интерполяция значений глубин осуществляется на основе сплайнов функции (3).
Алгоритм работы программного модуля: на вход подается файл в формате .txt, содержащий массив с изолиниями уровня глубин или точками, обозначающими глубины, далее строится схема четвертого порядка точности для оператора диффузионного переноса [20]. Полученные сеточные уравнения решаются адаптивным модифицированным попеременно-треугольным методом вариационного типа. На выходе получаем текстовый файл, содержащий массив значений глубин Азовского моря.
Результаты исследования. В результате исследования авторами получен среднесрочный прогноз распределения синезеленых и зеленых водорослей на основе комплексного подхода с использованием моделей динамики фитопланктонных популяций и гидродинамики. На рис. 2 представлен результат работы авторского алгоритма — восстановленная карта глубин Азовского моря.

Рис. 2. Полученное изображение рельефа дна Азовского моря
На основе разработанного метода также были получены пригодные для моделирования достаточно гладкие распределения значений солености и температуры, изображения которых приведены на рис. 3.
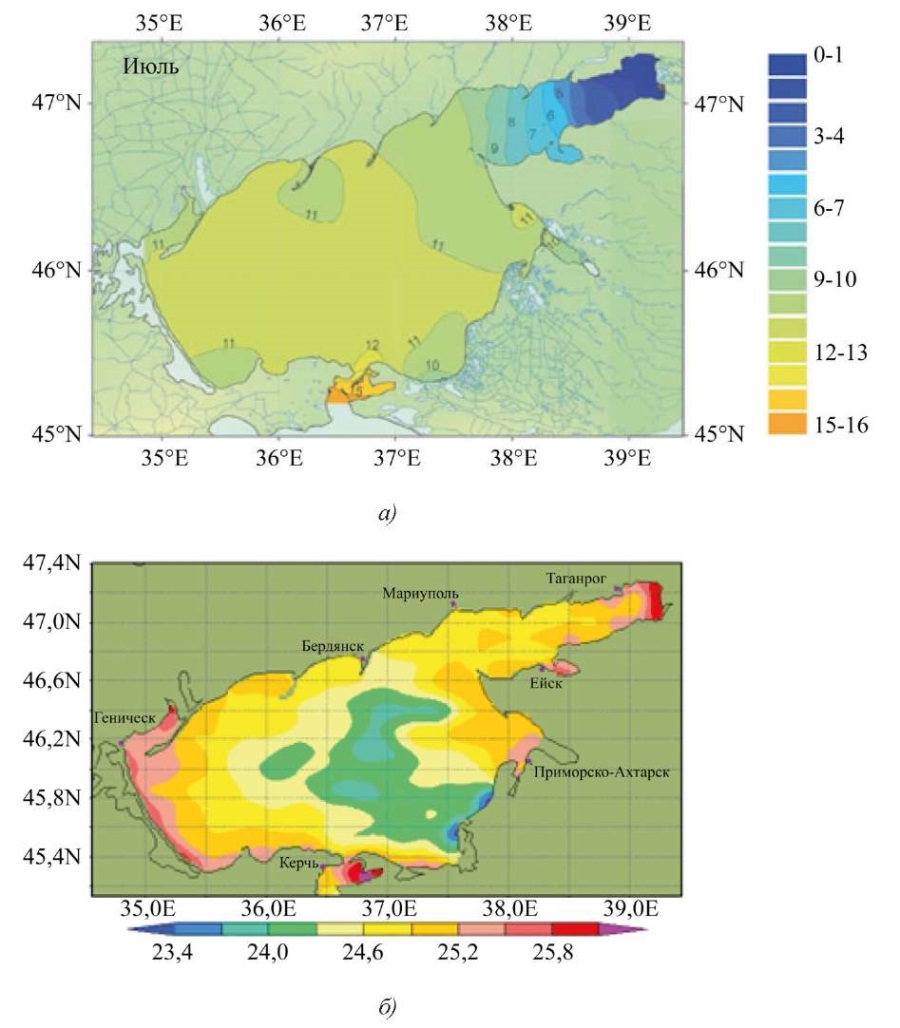
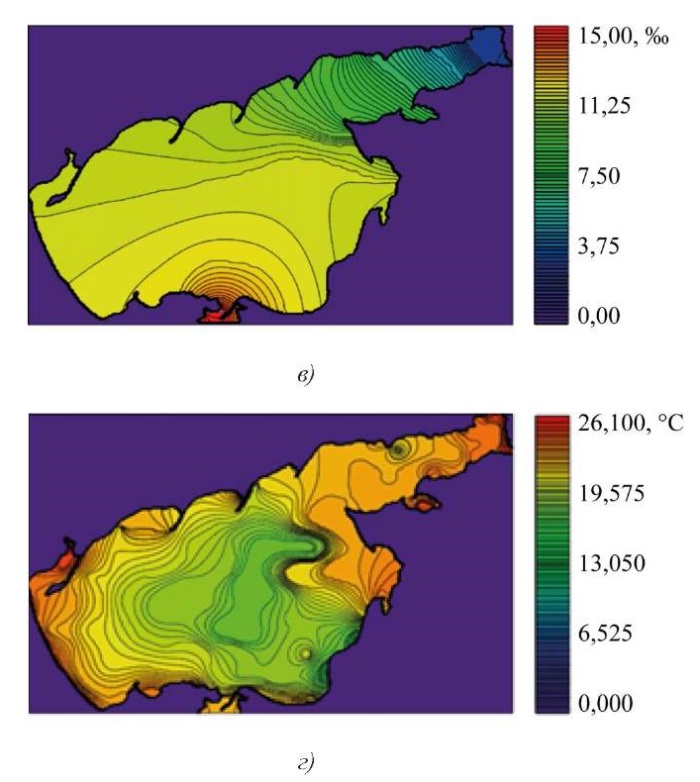
Рис. 3. Применение метода интерполяции:
а — начальное изображение изогалин [21];
б — начальное изображение изотерм2;
в — полученное изображение распределения солености S, ‰;
г — полученное изображение распределения температуры T, °C
Полученные распределения глубин, солености и температуры были использованы в качестве входных данных для решения задачи (1). На рис. 4 изображены концентрации двух фитопланктонных популяций, полученные в результате вычислительного эксперимента. В качестве входных данных для программного модуля подавались равномерные распределения моделируемых субстанций, временной интервал — 30 дней.
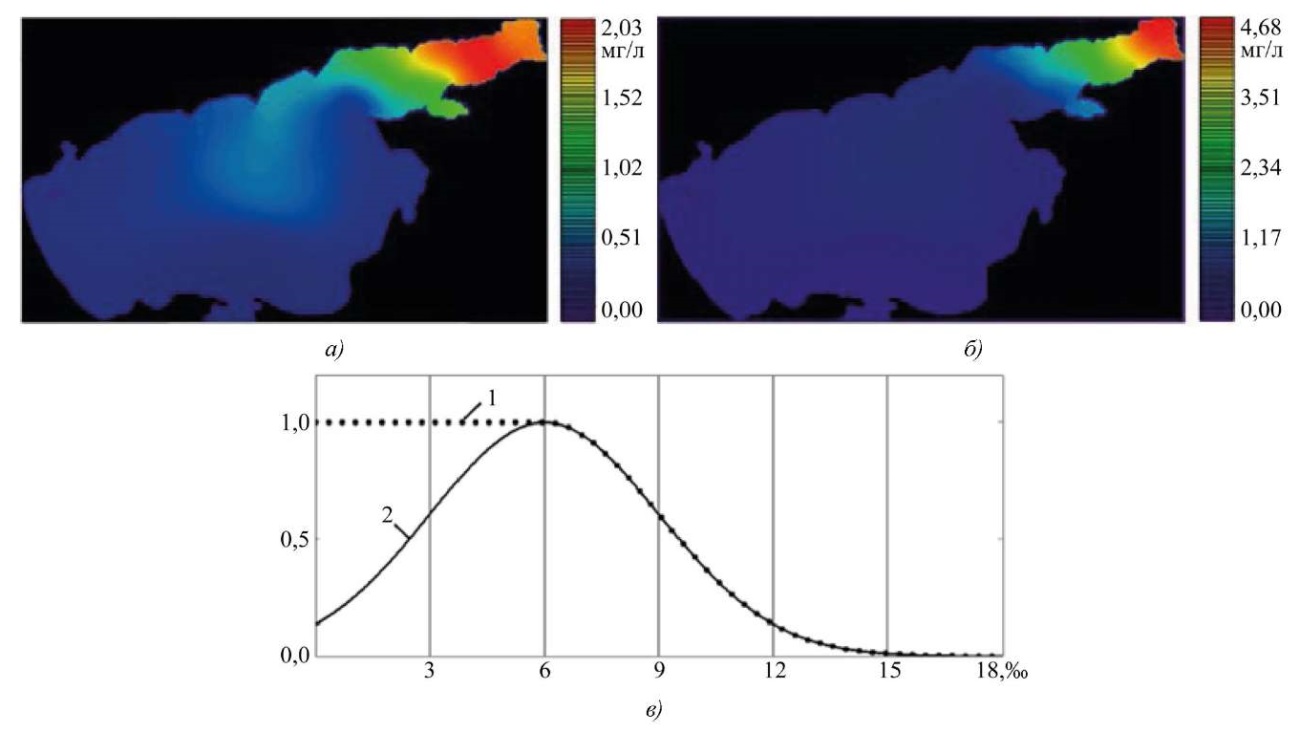
Рис. 4. Результаты решения задачи динамики фитопланктонных популяций:
а — распределение концентраций синезеленых водорослей q1, мг/л;
б — распределение концентраций зеленых водорослей q2, мг/л;
в — график зависимости коэффициента роста фитопланктонных популяций от солености S: 1 — зеленые; 2 — синезеленые водоросли
Обсуждение. Интерполяции распределения глубин, солености и температуры, полученные с помощью представленного авторами данной работы алгоритма, обладают достаточной степенью гладкости в точках склейки. Проведенный вычислительный эксперимент показал, что ареал у синезеленых водорослей шире, чем у зеленых водорослей — они распространены по всему Таганрогскому заливу и течениями выносятся в основную часть Азовского моря.
Математическая модель динамики фитопланктонных популяций учитывает ограничение питательными веществами развития микроводорослей, влияние гидрологического режима на значение коэффициента роста, географическую динамику под действием процессов конвекции и диффузии, кислородный режим. Использование данной модели в комплексе с моделью гидродинамики позволяет получить трехмерные изображения распределения моделируемых субстанций и учесть, помимо биологических особенностей развития фитопланктона, пространственно-временную динамику биомассы и особенности геометрии расчетной области.
Заключение. Описанная математическая модель и предложенные методы встроены в программный комплекс Azov3D, что позволяет прогнозировать развитие опасных цветений фитопланктонных популяций (эвтрофикацию) при различных погодных условиях, учитывать изменения солености, температуры, картины течений, наличие питательных веществ и кислородный режим. Построенные прогнозы могут быть использованы в выработке стратегии по управлению устойчивым развитием такого важного природного объекта, как Таганрогский залив. В настоящее время разрабатываются различные стратегии управления этой сложной водной экосистемой, определяются механизмы ее безопасности — возможные сценарии предотвращения заморных явлений и эвтрофикации. Методы математического моделирования, развитию которых посвящена данная статья, предоставляют относительно недорогой и оперативный инструментарий мониторинга и прогнозирования состояния водных экосистем.
1. Об утверждении Положения об осуществлении государственного мониторинга водных объектов. Постановление Правительства РФ № 219 от 10 апреля 2007 года. URL: https://docs.cntd.ru/document/902037173/titles/6560IO (дата обращения: 25.11.2025).
2. Оперативный модуль ЕСИМО. Температура поверхности воды в Азовском море. Единая государственная система информации об обстановке в мировом океане. URL: http://hmc.meteorf.ru/sea/azov/sst/sst_azov.html (дата обращения: 25.11.2025).
Список литературы
1. Ковалева Г.В. Проблема «цветения» воды в Азовском море. В: Труды Южного научного центра Российской академии наук. «Моделирование и анализ опасных природных явлений в Азовском регионе». Т. VIII. Ростов-на-Дону: Южный научный центр Российской академии наук; 2020. С. 122–148.
2. Overman C, Wells S. Modeling Cyanobacteria Vertical Migration. Water. 2022;14(6):953. https://doi.org/10.3390/w14060953
3. Gerbersdorf SU, Schubert H. Vertical Migration of Phytoplankton in Coastal Waters with Different UVR Transparency. Environmental Sciences Europe. 2011;23:36. https://doi.org/10.1186/2190-4715-23-36
4. Brookes JD, Ganf GG. Variations in the Buoyancy Response of Microcystis Aeruginosa to Nitrogen, Phosphorus and Light. Journal of Plankton Research. 2001;23(12):1399–1411. https://doi.org/10.1093/plankt/23.12.1399
5. Hongru Zhao, Wei Zhu, Huaimin Chen, Xiaohua Zhou, Ruo-Chen Wang, Ming Li. Numerical Simulation of the Vertical Migration of Microcystis (Cyanobacteria) Colonies Based on Turbulence Drag. Journal of Limnology. 2017;76(1):190–198. https://doi.org/10.4081/jlimnol.2016.1501
6. Chorus I, Welker M (eds.). Toxic Cyanobacteria in Water, 2nd edition. Boca Raton (FL): CRC Press; 2021. 858 p.
7. Матишов Г.Г., Фуштей Т.В. К проблеме вредоносных «цветений воды» в Азовском море. Электронный журнал «Исследовано в России». 2003;(6):213–225.
8. Man Xiao, Burford MA, Wood SA, Aubriot L, Ibelings BW, Prentice MJ, et al. Schindler's Legacy: From Eutrophic Lakes to the Phosphorus Utilization Strategies of Cyanobacteria. FEMS Microbiology Reviews. 2022;46(6):fuac029. https://doi.org/10.1093/femsre/fuac029
9. Wei Zhu, Ganyu Feng, Huaimin Chen, Ruochen Wang, Yongqin Tan, Hongru Zhao. Modelling the Vertical Migration of Different-Sized Microcystis Colonies: Coupling Turbulent Mixing and Buoyancy Regulation. Environmental Science and Pollution Research. 2018;25(30):30339–30347. https://doi.org/10.1007/s11356-018-3041-8
10. Zongpu Xue, Wei Zhu, Yuyang Zhu, Xihui Fan, Huaimin Chen & Ganyu Feng. Influence of Wind and Light on the Floating and Sinking Process of Microcystis. Scientific Reports. 2022;12:5655. https://doi.org/10.1038/s41598-022-08977-5
11. Fournier C, Fernandez-Fernandez R, Cirés S, López-Orozco JA, Besada-Portas E, Quesada A. LSTM Networks Provide Efficient Cyanobacterial Blooms Forecasting Even with Incomplete Spatio-Temporal Data. Water Research. 2024;267:122553. https://doi.org/10.1016/j.watres.2024.122553
12. Neverova G, Zhdanova O. Mathematical Modeling of the Evolutionary Dynamics of a Planktonic Community Using a Discrete-Time Model. Mathematics. 2023;11(22):4673. https://doi.org/10.3390/math11224673
13. Kang Peng, Zhixiong Hu, Rui Pang, Mingyue Li, Li Liu. Spatiotemporal Dynamics and Driving Factors of Phytoplankton Community Structure in the Liaoning Section of the Liao River Basin in 2010, 2015, and 2020. Water. 2025;17(15):2182. https://doi.org/10.3390/w17152182
14. Bo Li, Jing Li, Yuehang Hu, Shaozhe Cheng, Shouchun Li, Xuezhi Zhang. Algal Community Dynamics in Three Water Intakes of Poyang Lake: Implications for Drinking Water Safety and Management Strategies. Water. 2025;17(13):2034. https://doi.org/10.3390/w17132034.
15. Кудинов Н.В., Филина А.А., Никитина А.В., Бондаренко Д.В., Развеева И.Ф. Моделирование вертикальных движений морской воды в стратифицированных водоемах. Advanced Engineering Research (Rostov-on-Don). 2023;23(2):212–224. https://doi.org/10.23947/2687-1653-2023-23-2-212-224
16. Novikov M, Pakhomova S, Berezina A, Yakushev E. Model-Based Analysis of the Oxygen Budget in the Black Sea Water Column. Water. 2024;16(17):2380. https://doi.org/10.3390/w16172380
17. Yakushev EV, Pollehne F, Jost G, Kuznetsov I, Schneider B, Umlauf L. Analysis of the Water Column Oxic/Anoxic Interface in the Black and Baltic Seas with a Numerical Model. Marine Chemistry. 2007;107:388–410. https://doi.org/10.1016/j.marchem.2007.06.003
18. Сухинов А.И., Чистяков А.Е., Белова Ю.В., Кузнецова И.Ю. Аналитическое и численное исследование задачи динамики планктонных популяций при наличии микропластика. Математическое моделирование. 2024;36(3):95–114. https://doi.org/10.20948/mm-2024-03-07
19. Сухинов А.И., Кузнецова И.Ю. Математическая модель транспорта трехкомпонентной взвеси. Computational Mathematics and Information Technologies. 2023;7(3):39–48. https://doi.org/10.23947/2587-8999-2023-7-3-39-48
20. Чистяков А.Е., Семенякина А.А. Применение методов интерполяции для восстановления донной поверхности. Известия ЮФУ. Технические науки. 2013;4(141):21–28.
21. Матишов Г.Г., Бердников С.В., Жичкин А.П., Макаревич П.Р., Дженюк С.Л., Кулыгин В.В. и др. Атлас климатических изменений в больших морских экосистемах Северного полушария (1878–2013). Ростов-на-Дону: Южный научный центр РАН; 2014. 256 с.
Об авторах
Ю. В. БеловаРоссия
Юлия Валериевна Белова, кандидат физико-математических наук, доцент кафедры «Математика и информатика» Донского государственного технического университета
ElibraryID: 822411
ScopusID: 57196457293
ResearcherID: L-7893-2016
344003, г. Ростов-на-Дону, пл. Гагарина, 1
А. Е. Чистяков
Россия
Александр Евгеньевич Чистяков, доктор физико-математических наук, профессор кафедры «Программное обеспечение вычислительной техники и автоматизированных систем»
ElibraryID: 474527
ResearcherID: O-1507-2016
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Выполнено математическое прогнозирование роста водорослей в заливе. Построена трехмерная модель динамики вредных видов фитопланктона. Учет глубины, солености и температуры улучшил точность описания среды. Методы интерполяции дали гладкие поля глубины, солености и температуры. Получены трехмерные карты распространения цианобактерий и зеленых водорослей. Результаты пригодны для планирования охраны вод и управления прибрежной зоной.
Рецензия
Для цитирования:
Белова Ю.В., Чистяков А.Е. Моделирование динамики концентрации вредоносных видов фитопланктона в Таганрогском заливе Азовского моря. Безопасность техногенных и природных систем. 2025;9(4):284-293. https://doi.org/10.23947/2541-9129-2025-9-4-284-293. EDN: YTBWWQ
For citation:
Belova Yu.V., Chistyakov A.E. Modeling the Dynamics of Harmful Phytoplankton Species Concentration in Taganrog Bay of the Azov Sea. Safety of Technogenic and Natural Systems. 2025;9(4):284-293. https://doi.org/10.23947/2541-9129-2025-9-4-284-293. EDN: YTBWWQ
JATS XML








































